Cho tam giác ABC có góc B=1200; BC=12cm; AB=6cm, đường phân giác BD. Kẻ AH vuông góc đường thẳng BC(H thuộc đường thẳng BC). Tính tỉ số lượng giác của góc HAB, từ đó suy ra tỉ số lượng giác của góc ABH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phương pháp:
Xác định góc giữa các mặt phẳng (P) và (Q) ta thực hiện các bước sau:
+ Xác định giao tuyến d của (P) và (Q)
+ Trong mặt phẳng (P) xác định đường thẳng a ⊥ d trong mặt phẳng (Q) xác định đường thẳng b ⊥ d
+ Khi đó góc giữa (P) và (Q) là góc giữa hai đường thẳng a và b
Cách giải:
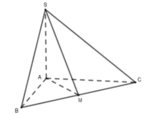
Gọi M là trung điểm BC => AM ⊥ BC (do ∆ ABC cân tại A).
Lại có ∆ SAB = ∆ SAC(c.g.c) hay ∆ SBC cân tại S
=> SM ⊥ BC
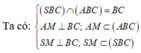
![]()
![]()

Theo đề bài
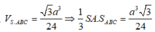
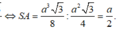
Lại thấy
∆
ABM vuông tại M có AB = a; ![]()
![]()
Xét tam giác SAM vuông tại A có SA = AM = a 2 nên ∆ SAM vuông cân tại A hay ∠ S M A = 45 °
Vậy góc giữa (SBC) và (ABC) bằng 45 °
Chọn D.
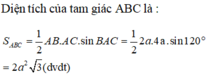
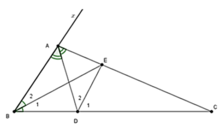



Vì \(\widehat{B}=120^0\) nên đường cao AH ứng với cạnh BC sẽ nằm ngoài tam giác ABC
Ta có: \(\widehat{ABH}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{ABH}+120^0=180^0\)
hay \(\widehat{ABH}=60^0\)
Xét ΔABH vuông tại H có
\(\widehat{ABH}=60^0\)(cmt)
nên \(\sin\widehat{ABH}=\dfrac{\sqrt{3}}{2}\); \(\cos\widehat{ABH}=\dfrac{1}{2}\); \(\tan\widehat{ABH}=\sqrt{3}\); \(\cot\widehat{ABH}=\dfrac{\sqrt{3}}{3}\)
Xét ΔABH vuông tại H có
\(\widehat{BAH}=30^0\)
nên \(\sin\widehat{BAH}=\dfrac{1}{2}\); \(\cos\widehat{BAH}=\dfrac{\sqrt{3}}{2}\); \(\tan\widehat{BAH}=\dfrac{\sqrt{3}}{3}\); \(\cot\widehat{BAH}=\sqrt{3}\)