Cho \(\Delta ABC\) có AB = 12; BC = 15; CA = 18. Gọi I là giao điểm của các đường phân giác trong \(\Delta ABC\), G là trọng tâm trong \(\Delta ABC\) . Tính IG = ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TM
3
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 3 2023
Kẻ phân giác AD (D thuộc BC)
\(\Rightarrow\widehat{B}=\widehat{BAD}=\widehat{CAD}=\dfrac{\widehat{A}}{2}\)
Xét hai tam giác ABC và DAC có:
\(\left\{{}\begin{matrix}\widehat{C}\text{ chung}\\\widehat{B}=\widehat{CAD}\end{matrix}\right.\) \(\Rightarrow\Delta ABC\sim\Delta DAC\left(g.g\right)\)
\(\Rightarrow\dfrac{AC}{DC}=\dfrac{BC}{AC}\Rightarrow DC=\dfrac{AC^2}{BC}=\dfrac{27}{4}\)
\(\Rightarrow BD=BC-DC=\dfrac{21}{4}\)
Áp dụng định lý phân giác:
\(\dfrac{BD}{AB}=\dfrac{DC}{AC}\Rightarrow AB=\dfrac{BD.AC}{DC}=7\)
3 tháng 3 2023
a: Xét ΔAMB vuông tại M và ΔANC vuông tạiN có
góc A chung
=>ΔAMB đồng dạng vơi ΔANC
=>AM/AN=AB/AC
=>AM*AC=AB*AN; AM/AB=AN/AC
b: Xét ΔAMN và ΔABC có
AM/AB=AN/AC
góc A chung
=>ΔAMN đồng dạng với ΔABC
=>góc AMN=góc ABC
26 tháng 1 2023
Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/3=CD/4
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{20}{7}\)
=>BD=60/7cm
I
10 tháng 11 2019
H B A C
Kẻ đường cao AH
ADHT về cạnh và góc vào △AHB vuông ở H có
AH=AB.cosB
⇒AH=12.sin42o
⇒AH\(\approx\)8(cm)
BH=AB.cosB=12.cos42\(\approx\)9(cm)
⇒HC=BC-BH=22-9=13(cm)
ADĐL pytago vào △AHC vuông ở H có
AH2+HC2=AC2
⇒82+132=AC2
⇒AC=\(\approx15,3\)(cm)
ADTSLG vào △AHC vuông ở H có
sinC=\(\frac{AH}{AC}=\frac{8}{15,3}\)
⇒\(\widehat{C}\)\(\approx\)36o
⇒\(\widehat{A}\)=102o
Ta có BC=BH+HC=12+18=30(cm)
ADHTvề cạnh và đường cao vào △ABCvuông ở C đường cao AH có
AH2=BH.CH=12.18=216
⇒AH=\(6\sqrt{6}\)(cm)
AB2=BH.BC=12.30=360
⇒AB=\(6\sqrt{10}\)(cm)
AC2=HC.AC=18.30=540
⇒AC=\(6\sqrt{15}\)(cm)
ADTSLG vào △AHC vuông ở H có
sinC=\(\frac{AH}{AC}=\frac{6\sqrt{6}}{6\sqrt{15}}\)
⇒C\(\approx\)39o
⇒\(\widehat{A}\)=81o
TT
1
20 tháng 2 2017
\(\frac{AB}{AC}=\frac{5}{12}\Leftrightarrow\frac{AB}{5}=\frac{AC}{12}=\frac{AC-AB}{12-5}=\frac{14}{7}=2\)
=> \(\hept{\begin{cases}AB=2.5=10\\AC=2.12=24\end{cases}}\)
Áp dụng Pitago => \(BC=\sqrt{AB^2+AC^2}=\sqrt{10^2+24^2}=26\)
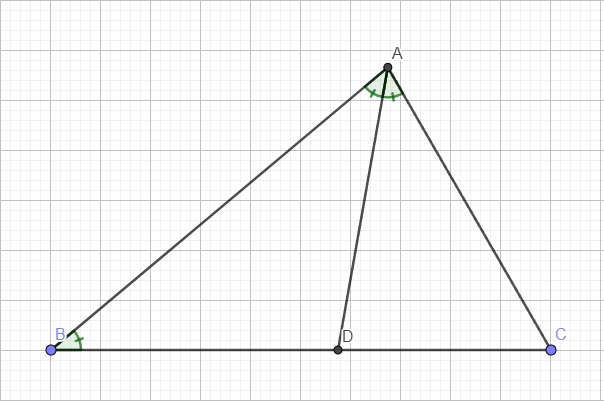
Gọi M là trung điểm của BC, D là chân đường phân giác kẻ từ A xuống BC
=>A,G,M thẳng hàng và A,I,D thẳng hàng
BM=CM=BC/2=7,5cm
AD là phân giác
=>BD/AB=CD/AC
=>BD/4=CD/6=15/10=1,5
=>BD=6cm
=>MD=1,5cm
IG//DM
=>IG/DM=AI/AD=2/3
=>IG=2/3DM=1cm