Cho tứ diện S.ABC có SA = AB = AC = a và AS; AB; AC vuông góc nhau từng đôi một. Tính diện tích mặt cầu ngoại tiếp tứ diện
A. S = πa 2 2
B. S = 3 πa 2 2
C. S = 3 πa 2 4
D. S = 3 πa 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
- Ta có:
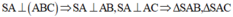 là các tam giác vuông.
là các tam giác vuông.
- Ta có: 
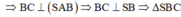 vuông tại B.
vuông tại B.
- Vậy hình chóp đã cho có cả 4 mặt đều là tam giác vuông.

Chọn A
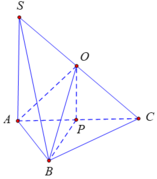
Ta có:
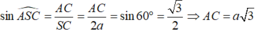
Do đó ![]() vuông tại B.
vuông tại B.
Gọi P là trung điểm của cạnh AC thì P là tâm đường tròn ngoại tiếp ΔABC.
Gọi O là trung điểm của cạnh SC => OS = OC
Ta có OP//SA mà ![]()
Do đó OP là trục đường tròn ngoại tiếp ΔABC => OA=OB=OC.
Như vậy
![]()

SA vg (ABC)=> SAB,SAC vuông
SA vg BC, AB vg BC => BCvg (SAB) =>SB vg BC=> SBC vuông
vậy all mặt đều vuông
\(\hept{\begin{cases}SA\perp\left(ABC\right)\\AB\subset\left(ABC\right)\end{cases}}\) \(\Rightarrow SA\perp AB\Rightarrow\) tam giác SAB vuông (1)
\(\hept{\begin{cases}SA\perp\left(ABC\right)\\AC\subset\left(ABC\right)\end{cases}\Rightarrow AC\perp SA\Rightarrow}\) tam giác SAC vuông (2)
Tam giác ABC vuông tại B (gt) (3)
\(\Rightarrow AB\perp BC\)
\(\hept{\begin{cases}SA\perp\left(ABC\right)\\BC\subset\left(ABC\right)\end{cases}\Rightarrow SA\perp BC}\)
\(\hept{\begin{cases}AB\perp BC\\SA\perp BC\end{cases}\Rightarrow\hept{\begin{cases}BC\perp\left(SAB\right)\\SB\subset\left(SAB\right)\end{cases}\Rightarrow}SB\perp BC\Rightarrow}\) Tam giác SBC vuông (4)
\(\left(1\right);\left(2\right);\left(3\right);\left(4\right)\Rightarrowđpcm\)

Đáp án B
V = 1 3 . S A . S A B C = 1 3 . S A . 1 2 . A B . A C . sin B A C = 1 3 . a . 1 2 . a . 2 a . sin 120 0 = a 3 3 6
Bán kính mặt cầu R 2 = a 2 2 2 + a 2 2 = 3 a 2 4
Diện tích mặt cầu S = 4 πR 2 = 4 π . 3 a 2 4 = 3 πa 2
Đáp án D