Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

4.
Gọi M là trung điểm CD, qua M kẻ đường thẳng song song AB
Gọi N là trung điểm AB, qua N kẻ đường thẳng song song AM
Gọi giao của 2 đường thẳng trên là O \(\Rightarrow\) O là tâm (S)
\(\Rightarrow AO=R=\sqrt{3}\)
Đặt \(AB=x;AC=y;AD=z\)
\(AN=\frac{AB}{2}=\frac{x}{2}\) ; \(AM=\frac{CD}{2}=\frac{1}{2}\sqrt{AC^2+AD^2}=\frac{1}{2}\sqrt{y^2+z^2}\)
Áp dụng Pitago: \(AO^2=AN^2+AM^2\)
\(\Rightarrow\frac{x^2}{4}+\frac{1}{4}\left(y^2+z^2\right)=3\Rightarrow x^2+y^2+z^2=12\)
\(V=\frac{1}{3}xyz\le\frac{1}{3}\left(\frac{x+y+z}{3}\right)^3\le\frac{1}{3}\left(\frac{\sqrt{3\left(x^2+y^2+z^2\right)}}{3}\right)^3=\frac{8}{3}\)
2.
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\)
\(AC=a\sqrt{2}\Rightarrow AO=\frac{1}{2}AC=\frac{a\sqrt{2}}{2}\)
\(SO=\sqrt{SA^2-OA^2}=\frac{a}{2}\)
Áp dụng công thức từ câu 1:
\(R=\frac{SA^2}{2SO}=\frac{3a}{4}\)
3.
\(BC=AB\sqrt{2}=2a\)
Gọi H là hình chiếu của S lên (ABC) \(\Rightarrow\) H đồng thời là tâm đường tròn ngoại tiếp đáy
\(\Rightarrow\) H là trung điểm BC
\(\Rightarrow\widehat{SAH}=60^0\Rightarrow SH=AH.tan60^0=\frac{BC}{2}tan60^0=a\sqrt{3}\)
\(SA=\frac{AH}{cos60^0}=2a\)
\(\Rightarrow R=\frac{SA^2}{2SH}=\frac{2\sqrt{3}a}{3}\)
\(S=4\pi R^2=\frac{16\pi a^2}{3}\)

Câu 5:
Tương tự câu 4, ta thấy tâm $I$ của khối cầu ngoại tiếp $S.ABCD$ là trung điểm $SC$
Theo định lý Pitago:
$SA^2=SB^2-AB^2=(a\sqrt{3})^2-a^2=2a^2$
$AC^2=AB^2+BC^2=a^2+a^2=2a^2$
$SC=\sqrt{SA^2+AC^2}=\sqrt{2a^2+2a^2}=2a$
Do đó: $R=SI=IC=\frac{SC}{2}=a$
Thể tích khối cầu ngoại tiếp S.ABCD là:
$V=\frac{4}{3}\pi R^3=\frac{4}{3}\pi a^3$
Đáp án A
Câu 4:
$AC=\sqrt{AB^2+AD^2}=2a$
$(SC, (ABCD))=\widehat{SCA}=60^0$
$\Rightarrow \frac{SA}{AC}=\tan \widehat{SCA}=\tan 60^0=\sqrt{3}$
$\Rightarrow SA=\sqrt{3}.AC=2\sqrt{3}a$
$SC=\sqrt{SA^2+AC^2}=\sqrt{(2\sqrt{3}a)^2+(2a)^2}=4a$
Gọi $I$ tâm mặt cầu ngoại tiếp hình chóp. $IS=IA=IC$ nên $I$ là tâm ngoại tiếp tam giác $SAC$
$\Rightarrow I$ là trung điểm $SC$.
Bán kính $IS=IC=\frac{AC}{2}=\frac{4a}{2}=2a$
Đáp án A

A E M B C H N S
Xét tam giác ABC có : \(BC=AB.\tan60^0=2a\sqrt{3}\Rightarrow S_{\Delta ABC}=2a^2\sqrt{3}\)
\(V_{S.ABCD}=\frac{1}{3}SA.S_{\Delta ABC}=\frac{1}{3}a\sqrt{3}.2a^2\sqrt{3}=2a^3\)
- Gọi N là trung điểm cạnh SA. Do SB//(CMN) nên d(SB. CM)=d(SB,(CMN))
=d(B,(CMN))
=d(A,(CMN))
- Kẻ \(AE\perp MC,E\in MC\) và kẻ \(AH\perp NE,H\in NE\), ta chứng minh được \(AH\perp\left(CMN\right)\Rightarrow d\left(A,\left(CMN\right)\right)=AH\)
Tính \(AE=\frac{2S_{\Delta AMC}}{MC}\) trong đó :
\(S_{\Delta AMC}=\frac{1}{2}AM.AC.\sin\widehat{CAM}=\frac{1}{2}a.4a\frac{\sqrt{3}}{2}=a^2\sqrt{3};MC=a\sqrt{13}\)
\(\Rightarrow AE=\frac{2a\sqrt{3}}{\sqrt{13}}\)
Tính được \(AH=\frac{2a\sqrt{3}}{\sqrt{29}}\Rightarrow d\left(A,\left(CMN\right)\right)=\frac{2a\sqrt{3}}{\sqrt{29}}\Rightarrow d\left(SB,CM\right)=\frac{2a\sqrt{3}}{\sqrt{29}}\)

S M H G N A O D C
Ta có \(\begin{cases}BC\perp SA\\BC\perp AB\end{cases}\)\(\Rightarrow BC\perp\left(SAB\right)\)\(\Rightarrow BC\perp AM\) (vì \(AM\subset\left(SAB\right)\left(1\right)\)
Mặt khác \(SC\perp\alpha\Rightarrow SA\perp AM\) (vì \(AM\subset\alpha\)) (2)
Từ (1) và (2) suy ra \(AM\perp\left(SBC\right)\Rightarrow AM\perp MG\) (vì \(MG\subset\left(SBC\right)\))
\(\Rightarrow\Delta AMG\) vuông tại M, tương tự ta cũng có tam giác ANG vuông tại N \(\Rightarrow\) tâm H đường tròn đáy của (H) là trung điểm AG, có bán kính \(R=\frac{AG}{2}\)
Xét tam giác vuông SAC tại A có \(AG=\frac{SA.AC}{SC}=\frac{\sqrt{6}}{3}a\Rightarrow R=\frac{\sqrt{6}}{6}a\)
Vì OH là đường cao (H)\(\Rightarrow OH\perp\alpha\Rightarrow OH\)//\(SC\Rightarrow O\) là giao điểm hai đường chéo AC, BD
\(\Rightarrow OH=\frac{1}{2}CG\).
Xét tam giác vuoongSAC có AG là đường cao, nên \(CG=\frac{AC^2}{SC}=\frac{2}{\sqrt{3}}a\Rightarrow OH=\frac{\sqrt{3}}{3}a\)
Vậy thể tích hình nón là \(V_{\left(H\right)}=\frac{1}{3}\pi.R^2.OH=\frac{\sqrt{3}}{54}\pi a^3\)

Dễ dàng chứng minh MN // BC
Xét \(\Delta SBC\) có MN // BC và MN đi qua trọng tâm G
\(\Rightarrow\) \(\begin{cases}SM=\frac{2}{3}SB\\SN=\frac{2}{3}SC\end{cases}\)
Sử dụng công thức tỉ lệ thể tích đố với 2 khối tứ diện S.AMN và S.ABC ta có
\(\frac{V_{S.AMN}}{V_{S.ABC}}=\frac{SA}{SA}.\frac{SM}{SB}.\frac{SN}{SC}=1.\frac{2}{3}.\frac{2}{3}=\frac{4}{9}\\ \Rightarrow V_{S.AMN}=\frac{4}{9}.V_{S.ABC}\)
Tính được \(V_{S.ABC}=\frac{1}{6}SA.AB.BC=\frac{a^3}{6}\)
\(\Rightarrow V_{S.AMN}=\frac{2a^3}{27}\)

Lời giải:
Gọi $H$ là chân đường cao kẻ từ $S$ xuống mặt phẳng $(ABC)$
Ta có \(\left\{\begin{matrix} SH\perp AB\\ SA\perp AB\end{matrix}\right.\Rightarrow AB\perp (SHA)\rightarrow AB\perp HA\)
Tương tự \(BC\perp HC\). Kết hợp với \(ABC\) vuông cân tại $B$ suy ra \(ABCH\) là hình vuông
Có \(AH\parallel (SBC)\Rightarrow d(A,(SBC))=d(H,(SBC))\)
Kẻ \(HT\perp SC\). Có \(\left\{\begin{matrix} SH\perp BC\\ HC\perp BC\end{matrix}\right.\Rightarrow BC\perp (SHC)\Rightarrow BC\perp HT\)
Do đó \(HT\perp (SBC)\Rightarrow d(H,(SBC))=HT=\sqrt{\frac{SH^2.HC^2}{SH^2+HC^2}}=\sqrt{\frac{SH^2.AB^2}{SH^2+AB^2}}=\sqrt{2}\Rightarrow SH=\sqrt{6}a\)
Từ trung điểm $O$ của $AC$ dựng trục vuông góc với mặt phẳng $(ABC)$. Trên trục đó ta lấy điểm $I$ là tâm mặt cầu ngoại tiếp.
\(IS^2=IA^2=IH^2\Leftrightarrow (\overrightarrow{IO}+\overrightarrow{OH}+\overrightarrow{HS})^2=IO^2+OH^2\)
\(\Leftrightarrow HS^2+2\overrightarrow{IO}.\overrightarrow{HS}=0\)
Do \(\overrightarrow {SH}\parallel \overrightarrow {IO}\Rightarrow \overrightarrow {IO}=k\overrightarrow{SH}\). Thay vào PT trên có $k=\frac{1}{2}$
\(\Rightarrow IO=\frac{\sqrt{6}a}{2}\Rightarrow IA=\sqrt{IO^2+AO^2}=\sqrt{3}a\)
\(\Rightarrow S_{\text{mặt cầu}}=4\pi R^2=12a^2\pi\)


Chọn A
Ta có:
Do đó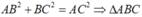 vuông tại B.
vuông tại B.
Gọi P là trung điểm của cạnh AC thì P là tâm đường tròn ngoại tiếp ΔABC.
Gọi O là trung điểm của cạnh SC => OS = OC
Ta có OP//SA mà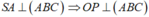
Do đó OP là trục đường tròn ngoại tiếp ΔABC => OA=OB=OC.
Như vậy