Cho tam giác ABC có AB = 6; AC = 8 ; BC = 10. Gọi M,N,P tương ứng là chân đường cao , chấn đường phân giác , chân đường trung tuyến kẻ từ đỉnh A
a) Chứng mình rằng , điểm N nằm giữa hai điểm M và P
b) Tính diện tích các tam giác ABP , ANB và ABM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác ABC và tam giác AED có
\(\hept{\begin{cases}A:gócchung\\\frac{AE}{AB}=\frac{AD}{AC}\left(\frac{8}{20}=\frac{6}{15}\right)\end{cases}}\)
Vậy tam giác ABC đồng dạng với tam giác AED (c-g-c)
easy :>
A B C D E
Ta có : \(\frac{AE}{AB}=\frac{6}{15}=\frac{2}{5} ;\frac{ AD}{AC}=\frac{8}{20}=\frac{2}{5}\)
\(\Rightarrow\frac{AE}{AB}=\frac{AB}{AC}\)
Xét 2 tam giác : ADE và ACB có :
\(\widehat{A}\)chung
\(\frac{AE}{AB}=\frac{AB}{AC}\)
\(\Rightarrow\Delta ADE~\Delta ACB\left(TH2\right)\)

Nửa chu vi tam giác ABC là: p = 4 + 6 + 8 2 = 9
Áp dụng công thức Hê- rông, diện tích tam giác ABC:
S = 9 9 − 4 9 − 6 9 − 8 = 3 15
ĐÁP ÁN A

Diện tích tam giác ABC là:
S = 1 2 A B . A C . sin A = 1 2 .5.6. sin 30 ° = 15 2
Chọn A

Diện tích tam giác ABC là:
S = 1 2 A B . A C . sin A = 1 2 .4.6. sin 30 0 = 6
ĐÁP ÁN B

Áp dụng định lý Py-ta-go đảo vào tam giác ABC, có:
AB2 + AC2 = 62 + 82 = 100 = 102 = BC2
Suy ra tam giác ABC vuông
!
+ Xét tam giác ABC có :
AB^2+AC^2=100
BC^2=10^2=100
=> AB^2+ AC^2= 100=BC^2
=> tam giác ABC vuông tại A ( Py-ta-go)

ko biết em mới lớp 5 k em nha có câu kính trên nhường dưới mà đúng ko

Ta có: AB/AC=3/4 => AB/3=AC/4
=>. Đặt AB/3=AC/4=k
=> AB=3k ; AC=4k
Vì tg ABC vuông tại A
Áp dụng định lý Py-ta-go vào tg vuông ABC ta có:
=> AB^2 + AC^2 = BC^2
=> (3k)^2 + (4k)^2 = 15^2
=> 9k^2 + 16k^2 = 225
=> 25k^2 = 225
=> k^2=9 => k=3
=> AB=3k=3.3=9 cm
AC=4k=4.3=12 cm

a. Ta có:
AB2 + AC2 = 32 + 42 = 25 = 52 = BC2
Tam giác ABC vuông tại A (theo định lí Pytago đảo) (2 điểm)
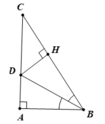
A B C M N P
Nhận xét: AB2 + AC2 = BC2 (Vì 62 + 82 = 102) => tam giác ABC vuông tại A (theo ĐL Pi ta go)
Trong tam giác vuông ABC có: AB2 = BM.BC => BM = 62 : 10 = 3,6
AN là p/g của góc A => BN/ NC = AB/AC = 6/8 = 3/4 => BN = 3/4 . NC
Có BN + NC = BC => (3/4). NC + NC = BC = 10 => 7/4 . NC = 10 => NC = 40/7 => BN = 10 - 40/7 = 30/7
BP là trung tuyến nên P là trung điểm của BC => BP = BC/ 2 = 5
Trên tia BC có: BM < BN < BP (3,6 < 30/7 < 5) => N nằm giữa M và P
b) Ta có: AM. BC = AB . AC => AM = 6.8 : 10 = 4,8
=> S(ABP) = AM . BP : 2 = 4,8 . 5 : 2 = 12
S(ANP) = AM . BP : 2 = ...
S(ABM) = AM . BM : 2 = ....(thay số )