Tìm giá trị nhỏ nhất của hàm số y = x + trên đoạn [2;4].
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có:
x + 2 ≥ 0 , x + 2 = 0 ⇔ x = − 2 ∈ − 3 ; 3 ⇒ min − 3 ; 3 y = 0

\(y=4\left(x-2\right)+\dfrac{9}{x-2}+8\ge2\sqrt{\dfrac{36\left(x-2\right)}{x-2}}+8=20\)
\(y_{min}=20\) khi \(x=\dfrac{7}{2}\)

Đáp án B
PT hoành độ giao điểm là:
x 3 + 2 x 2 + 5 x + 1 = 3 x + 1 ⇔ x = 0 x 2 + 2 x + 2 = 0 ⇒ x 0 = 0 ⇒ y 0 = 1.
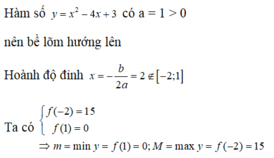
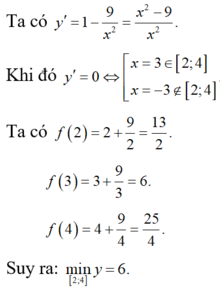
Chọn C
Ta có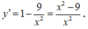
Khi đó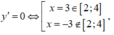
Ta có
Suy ra: m i n y [ 2 ; 4 ] = 6