Trong không gian với hệ tọa độ Oxyz, cho ba điểm và . Tìm m để tam giác MNP vuông tại N.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Do M ∈ O z ⇒ M 0 ; 0 ; a ⇒ M A → = 1 ; 1 ; 3 - a , M B → = 0 ; 2 ; 1 - a , M C → = - 2 ; 0 ; - 3 - a
⇒ 2 M A → + M B → + M C → = 0 ; 4 ; - 4 a + 4 ⇒ 2 M A → + M B → + M C → = 4 a - 1 2 + 1 ≥ 4 xảy ra khi a = 1.
Do đó tọa độ điểm M là M(0;0;1).

Đáp án A.
M là điểm thuộc tia đối của tia BA sao cho A M B M = 2 nên B là trung điểm của AM.


Chọn B
Đặt M(x;y;z). Lập hệ 3 phương trình ba ẩn x,y,z từ phương trình mặt phẳng (P) và điều kiện MA=MB, MA=MC

Đáp án C
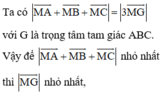
hay M là hình chiếu của G lên mặt phẳng (P).
Ta có G(1;0;2), ta tìm hình chiếu của G lên mặt phẳng (P) bằng cách tìm giao điểm của đường thẳng qua G vuông góc với mặt phẳng (P) với mặt phẳng (P).
Phương trình đường thẳng qua điểm G và vuông góc với mặt phẳng (P)
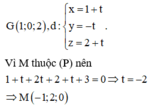





Đáp án D.
Ta có: N M ¯ = 3 ; 1 ; 5 N P ¯ 2 ; m − 1 ; 1 do đó tam giác MNP vuông tại N khi
N M ¯ . N P ¯ = 6 + 1. m − 1 + 5 = 0
⇔ m = − 10.