Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Đặt M(x;y;z). Lập hệ 3 phương trình ba ẩn x,y,z từ phương trình mặt phẳng (P) và điều kiện MA=MB, MA=MC

Đáp án B
Phương pháp: (P) cách đều B, C ó d(B;(P)) = d(c;(P))
TH1: BC // (P)
TH2: I ∈ (P), với I là trung điểm của BC
Cách giải:
Ta có: ![]()
(P) cách đều B, C ó d(B;(P)) = d(c;(P))
TH1: BC // (P)
![]()
=> (P) đi qua O và nhận ![]() là 1 VTPT
là 1 VTPT
![]()
TH2: I ∈ (P) với I là trung điểm của BC
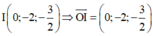
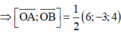
=> (P): 6x – 3y + 4z = 0
Dựa vào các đáp án ta chọn được đáp án B

Đáp án A
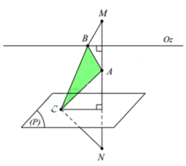
Gọi M, N lần lượt là hai điểm đối xứng với A qua Oz và mặt phẳng (P) ( hình vẽ bên: Điểm A nằm giữa Oz, (P) vì O, A cùng phía với (P) và d O z ; P > d A ; P .
Khi đó C Δ A B C = A B + B C + A C = B M + B C + C N
Suy ra B M + B C + C N min ⇒ B , C , M , N thẳng hàng.
Hay B là hình chiếu của A trên Oz, Vậy B 0 ; 0 ; 1
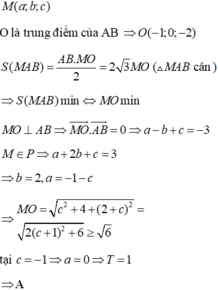

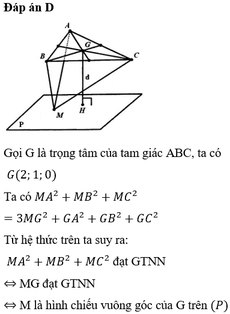





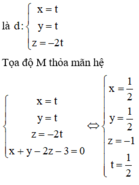
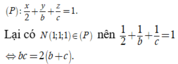
Đáp án C.
Do M ∈ O z ⇒ M 0 ; 0 ; a ⇒ M A → = 1 ; 1 ; 3 - a , M B → = 0 ; 2 ; 1 - a , M C → = - 2 ; 0 ; - 3 - a
⇒ 2 M A → + M B → + M C → = 0 ; 4 ; - 4 a + 4 ⇒ 2 M A → + M B → + M C → = 4 a - 1 2 + 1 ≥ 4 xảy ra khi a = 1.
Do đó tọa độ điểm M là M(0;0;1).