Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
ĐKXĐ: \(x>1\)
\(log_2\left(x-1\right)+log_2\left(x+1\right)=3\)
\(\Leftrightarrow log_2\left(x-1\right)\left(x+1\right)=3\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)=8\)
\(\Leftrightarrow x^2-9=0\Rightarrow\left[{}\begin{matrix}x=3\\x=-3< 1\left(l\right)\end{matrix}\right.\)
Vậy tập nghiệm của pt là \(S=\left\{3\right\}\)
Khoảng giá trị của x mà đồ thị hàm số \(y=log_2x\) nằm phía trên đường thẳng y = 2 là \(\left(4;+\infty\right)\)
\(\Rightarrow\) Tập nghiệm của bất phương trình \(log_2x>2\) là \(\left(4;+\infty\right)\)
Để \(logx\) xác định \(\Rightarrow x>0\Rightarrow log\left|x\right|=logx\)
Pt tương đương:
\(logx=\left|logx\right|\Leftrightarrow logx>0\Rightarrow x>1\)
\(\Rightarrow S=\left(1;+\infty\right)\)
ĐK: x>1
\(\log_{2^{\dfrac{1}{2}}}\left(x-1\right)+\log_{2^{-1}}\left(x+1\right)=1\)
\(\log_2\left[\left(x-1\right)^2.\left(x-1\right)^{-1}\right]=\log_22\)
=> x-1 = 2(x-1)
=> x=1 (ktmđk)
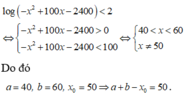
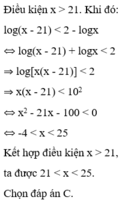
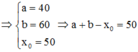
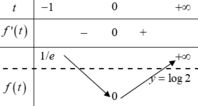
Đáp án D
Ta có log x = log x ⇔ x > 0 log x = log x ⇔ log x ≥ 0 log x = log x log x = − log x ⇔ x ≥ 1 log x = 0 ⇔ x ≥ 1 x = 10