Cho phương trình – 2(m + 4)x + – 8 = 0. Xác định m để phương trình có hai nghiệm thỏa mãn đạt giá trị lớn nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x2-2(m-1)x+m2-3m=0
△'=[-(m-1)]2-1(m2-3m)=(m-1)2-(m2-3m)=m2-2m+1-m2+3m= m+1
áp dụng hệ thức Vi-ét ta được
x1+x2=2(m-1) (1)
x1*x2=m2-3m (2)
a) để PT có 2 nghiệm phân biệt khi m+1>0 <=> m>-1
b) để PT có duy nhất một nghiệm âm thì x1*x2 <0
e) Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)=2m-2\\x_1x_2=m^2-3m\end{matrix}\right.\)
Ta có: \(x_1^2+x_2^2=8\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=8\)
\(\Leftrightarrow\left(2m-2\right)^2-2\cdot\left(m^2-3m\right)-8=0\)
\(\Leftrightarrow4m^2-8m+4-2m^2+6m-8=0\)
\(\Leftrightarrow2m^2-2m-4=0\)(1)
\(\Delta=\left(-2\right)^2-4\cdot2\cdot\left(-4\right)=4+32=36\)
Vì \(\Delta>0\) nên phương trình (1) có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}m_1=\dfrac{2-\sqrt{36}}{4}=\dfrac{2-6}{4}=-1\\m_2=\dfrac{2+\sqrt{36}}{4}=\dfrac{2+6}{4}=2\end{matrix}\right.\)
Vậy: Để phương trình có hai nghiệm phân biệt thỏa mãn \(x_1^2+x_2^2=8\) thì \(m\in\left\{-1;2\right\}\)

x2 - 2(m - 1)x +m2 + 4m + 13 = 0 (1) \(\left(a=1;b=-2\left(m-1\right);c=m^2+4m+13\right)\)
Ta có \(\Delta'=\left(-\left(m-1\right)\right)^2-1.\left(m^2+4m+13\right)\)
\(=m^2-2m+1-m^2-4m-13\)
\(=-6m-12=-6\left(m+2\right)\)
a+b, Để phương trình (1) có nghiệm \(\Leftrightarrow\Delta'\ge0\Leftrightarrow-6\left(m+2\right)\ge0\)
\(\Leftrightarrow m+2\le0\)
\(\Leftrightarrow m\le-2\)
Câu b giống với câu a nhé!

a. Bạn tự giải
b. Pt có nghiệm kép khi:
\(\Delta'=\left(m+1\right)^2-4m=0\Leftrightarrow m^2-2m+1=0\Leftrightarrow m=1\)
Khi đó: \(x_{1,2}=m+1=2\)
c. Do pt có nghiệm bằng 4:
\(\Rightarrow4^2-2\left(m+1\right).4+4m=0\)
\(\Leftrightarrow8-4m=0\Rightarrow m=2\)
\(x_1x_2=4m\Rightarrow x_2=\dfrac{4m}{x_1}=\dfrac{4.2}{4}=2\)

a: Khi m=1 thì pt sẽ là: x^2+4x-3=0
=>x=-2+căn 7 hoặc x=-2-căn 7
b: Δ=(2m-6)^2-4(m-4)
=4m^2-24m+36-4m+16
=4m^2-28m+52=(2m-7)^2+3>0
=>PT luôn có hai nghiệm pb
c: PT có hai nghiệm trái dấu
=>m-4<0
=>m<4

Phương trình có hai nghiệm trái dấu khi và chỉ khi ![]() suy ra m < -2.
suy ra m < -2.
Tổng của hai nghiệm bằng -3 khi ![]() thỏa mãn điều kiện m < -2.
thỏa mãn điều kiện m < -2.
Đáp số: m = -5.

a) Xét pt \(x^2-\left(2m-3\right)x+m^2-3m=0\)
Ta có \(\Delta=\left[-\left(2m-3\right)^2\right]-4.1\left(m^2-3m\right)\)\(=4m^2-12m+9-4m^2+12m\)\(=9>0\)
Vậy pt đã cho luôn có 2 nghiệm phân biệt với mọi m.
Câu b mình nhìn không rõ đề, bạn sửa lại nhé.


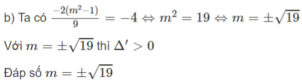
Phương trình x 2 – 2(m + 4)x + m 2 – 8 = 0 có a = 1 ≠ 0 và
∆ ' = ( m + 4 ) 2 – ( m 2 – 8 ) = 8 m + 24
Phương trình có hai x 1 ; x 2 ⇔ ∆ ' ≥ 0 ⇔ 8 m + 24 ≥ 0
Áp dụng định lý Vi – ét ta có x 1 + x 2 = 2 ( m + 4 ) ; x 1 . x 2 = m 2 – 8
Ta có:
A = x 1 + x 2 − 3 x 1 x 2
= 2 (m + 4) – 3 ( m 2 – 8) = 3 m 2 + 2m + 32 = − 3 m 2 − 2 3 m − 32 3
= − 3 m − 1 3 2 + 97 3
Nhận thấy A ≤ 97 3 và dấu “=” xảy ra khi m − 1 3 = 0 ⇔ m = 1 3 (TM)
Vậy giá trị lớn nhất của A là 97 3 khi m = 1 3
Đáp án: A