Dùng đồ thị hàm số, hãy cho biết:
a) Với mỗi \(m \in \left[ { - 1;1} \right]\), có bao nhiêu giá trị \(\alpha \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho \(\sin \alpha = m\)
b) Với mỗi \(m \in \left[ { - 1;1} \right]\), có bao nhiêu giá trị \(\alpha \in \left[ {0;\pi } \right]\) sao cho \(\cos \alpha = m\)
c) Với mỗi \(m \in \mathbb{R}\), có bao nhiêu giá trị \(\alpha \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho \(\tan \alpha = m\)
d) Với mỗi \(m \in \mathbb{R}\), có bao nhiêu giá trị \(\alpha \in \left[ {0;\pi } \right]\) sao cho \(\cot \alpha = m\)


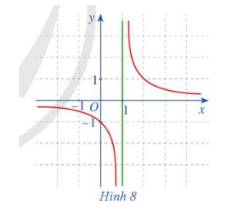
a) Đồ thị hàm số:
- Với mỗi \(m \in \left[ { - 1;1} \right]\) chỉ có 1 giá trị \(\alpha \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho \(\sin \alpha = m\)
b) Đồ thị hàm số:
- Với mỗi \(m \in \left[ { - 1;1} \right]\) có 1 giá trị \(\alpha \in \left[ {0;\pi } \right]\) sao cho \(\cos \alpha = m\)
c) Đồ thị hàm số:
- Với mỗi \(m \in \mathbb{R}\), có 2 giá trị \(\alpha \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho \(\tan \alpha = m\)
d) Đồ thị hàm số:
- Với mỗi \(m \in \mathbb{R}\), có 2 giá trị \(\alpha \in \left[ {0;\pi } \right]\) sao cho \(\cot \alpha = m\)