Cho \(\widehat{xoy}=\alpha;\)\(\widehat{xoz}=\beta\)\((\alpha>\beta)\)
Gọi om là tia phân giác của \(\widehat{yoz}\). Tính \(\widehat{xom}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C K H I D U V E F
Gọi giao điểm của Ax với cạnh BC là V, trung trực của BC cắt AC,BC lần lượt tại H,F
Phân giác ^BAK cắt BH tại U. Trung trực của BH cắt BH và AU lần lượt tại E và I
Từ giả thiết ta có ^ABC = 2.^ACB. Do H thuộc trung trực của BC nên ^HBC = ^HCB = ^ACB
=> ^ABC = 2.^HBC hay ^ABH = ^ACB. Từ đó \(\Delta\)AHB ~ \(\Delta\)ABC (g.g)
Dễ thấy ^BAU = ^CAV = ^BAC/3, ^ABU = ^ACV => \(\Delta\)AUB ~ \(\Delta\)AVC (g.g)
Do đó \(\frac{BU}{CV}=\frac{AB}{AC}=\frac{BH}{CB}=\frac{BE}{CF}=\frac{BU-BE}{CV-CF}=\frac{EU}{FV}\)
Cũng dễ có \(\Delta\)IEU ~ \(\Delta\)KFV (g.g) => \(\frac{EU}{FV}=\frac{IU}{KV}\). Suy ra \(\frac{BU}{CV}=\frac{IU}{KV}\)
Kết hợp với ^IUB = ^KVC (^AUB = ^AVC) dẫn tới \(\Delta\)BIU ~ \(\Delta\)CKV (c.g.c)
=> ^IBU = ^KCV hay ^IBH = ^KCB. Mà hai tam giác BIH và BKC cân tại I và K nên \(\Delta\)BIH ~ \(\Delta\)BKC
Từ đây \(\Delta\)BIK ~ \(\Delta\)BHC (c.g.c). Có \(\Delta\)BHC cân tại H => \(\Delta\)BIK cân tại I
Nếu ta lấy một điểm D sao cho ^BID = ^IKA, ^IBD = ^KIA thì \(\Delta\)IBD = \(\Delta\)KIA (g.c.g)
=> ^BDI = ^IAK = ^IAB => Từ giác AIBD nội tiếp. Đồng thời có AI = BD nên AIBD là hình thang cân
=> AB = DI. Mà DI = AK (vì \(\Delta\)IBD = \(\Delta\)KIA) nên AB = AK => \(\Delta\)BAK cân tại A
=> ^AKB = (1800 - ^BAK)/2 = \(\frac{180^0-2\alpha}{2}=90^0-\alpha=90^0-\frac{180^0-3\beta}{3}=30^0+\beta\)
Vậy \(\widehat{AKB}=90^0-\alpha=30^0+\beta\).

Ta có: xOy+zOy=xOy ( Oz nằm giữa Ox và Oy )
=> yOz= xOy-xOz=100-40=60(độ)

Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOz}< \widehat{xOy}\left(40^0< 100^0\right)\)
nên tia Oz nằm giữa hai tia Ox và Oy
\(\Leftrightarrow\widehat{xOz}+\widehat{yOz}=\widehat{xOy}\)
\(\Leftrightarrow\widehat{yOz}+40^0=100^0\)
hay \(\widehat{yOz}=60^0\)
Vậy: \(\widehat{yOz}=60^0\)

Từ N kẻ đường thẳng z đi qua N song song vs Mx( Hình phụ các cậu tự vẽ vào nhé)
\(\Rightarrow Nz//Mx\)(1)
\(\Rightarrow\widehat{NMx}=\widehat{MNz}\left(=\alpha\right)\left(SLT\right)\)(Vì \(\widehat{NMx}=\alpha\left(gt\right)\))
Lại có: \(\widehat{MNP}=\widehat{MNz}+\widehat{PNz}=\alpha+\beta\), mà\(\widehat{MNz}=\alpha\left(cmt\right)\Rightarrow\widehat{PNz}=\beta\), mà \(\widehat{NPy}=\beta\left(gt\right)\Rightarrow\widehat{NPz}=\widehat{NPy}\), Mà 2 góc ở vị trí SLT \(\Rightarrow Nz//Py\left(2\right)\)
Từ (1) và (2) \(\Rightarrow Mx//Py\)Hay \(x//y\)
Vậy...

Vì hai góc \(\widehat {xOy},\widehat {yOz}\) kề bù với nhau nên
\(\begin{array}{l}\widehat {xOy} + \widehat {yOz} = 180^\circ \\ \Rightarrow 25^\circ + \widehat {yOz} = 180^\circ \\ \Rightarrow \widehat {yOz} = 180^\circ - 25^\circ = 155^\circ \end{array}\)

Tham khảo:
Trường hợp 1: \(\alpha = {90^o}\)
Khi đó \({90^o} - \alpha = {0^o}\)
Tức là M và N lần lượt trùng nhau với B và A.
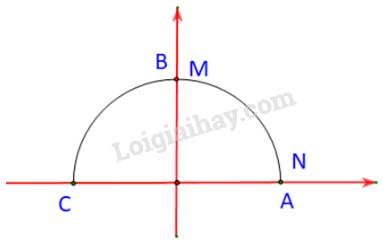
Và \(\cos \alpha = 0 = \sin \left( {{{90}^o} - \alpha } \right)\)
Trường hợp 2: \({0^o} < \alpha < {90^o} \Rightarrow {0^o} < {90^o} - \alpha < {90^0}\)
M và N cùng nằm bên trái phải trục tung.
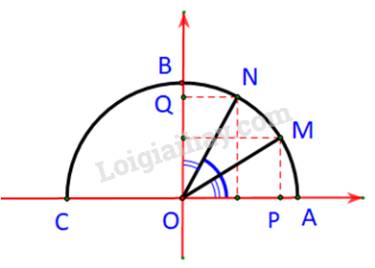
Ta có: \(\alpha = \widehat {AOM};\;\;{90^o} - \alpha = \widehat {AON}\)
Dễ thấy: \(\widehat {AON} = {90^o} - \alpha = {90^o} - \widehat {NOB}\;\;\; \Rightarrow \alpha = \widehat {NOB}\)
Xét hai tam giác vuông \(NOQ\) và tam giác \(MOP\) ta có:
\(OM = ON\)
\(\widehat {POM} = \widehat {QON}\)
\(\begin{array}{l} \Rightarrow \Delta NOQ = \Delta MOP\\ \Rightarrow \left\{ \begin{array}{l}OP = OQ\\QN = MP\end{array} \right.\end{array}\)
Mà \(M\left( {{x_0};{y_o}} \right)\) nên \(N\left( {{y_o};{x_0}} \right)\). Nói cách khác:
\(\cos \left( {{{90}^o} - \alpha } \right) = \sin \alpha ;\;\;\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha .\)