NEED HELP!!!
Tìm nghiệm số phức;
\(z^4+4z^3+11z^2+14z+10=0\)
biết nghiệm :
\(z1=-1+i\)
\(z2=-1-i\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 3 2018
Chọn C.
+ Ta có
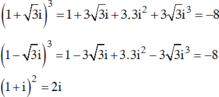
Do đó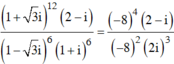 
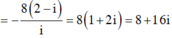
Theo giả thiết ta có ( 8 + 16i) 2 + 8b( 8 + 16i) + 64c = 0
Tương đương: ( 1 + 2i) 2 + b( 1 + 2i) + c = 0
Hay ( 2b + 4)i + b + c – 3 = 0
Ta có hệ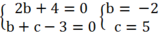 
Khi đó:
CM
6 tháng 8 2018
Đáp án B
z 2 + 6 z + 13 = 0 ⇔ z = − 3 ± 2 i ⇒ z 1 = − 3 − 2 i z 2 = − 3 + 2 i w = z 1 + 2 z 2 = − 9 + 2 i
CM
23 tháng 11 2019
Đáp án B
z 2 + 6 z + 13 = 0 ⇔ z = − 3 ± 2 i ⇒ z 1 = − 3 − 2 i z 2 = − 3 + 2 i w = z 1 + 2 z 2 = − 9 + 2 i
CM
23 tháng 8 2019
Đáp án B.
Phương pháp giải: Giải phương trình bậc hai tìm nghiệm phức
Lời giải:
Ta có:
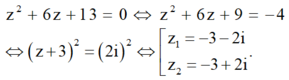
Vậy 
Lời giải:
Vì phương trình có nghiệm \(z_1=-1+i, z_2=-1-i\) nên bằng định lý Viete đảo ta có một nhân tử của phương trình là \(z^2+2z+2\)
Do đó dễ dàng phân tích phương trình trên như sau:
\(z^4+4z^3+11z^2+14z+10=0\)
\(\Leftrightarrow (z^2+2z+2)(z^2+2z+5)=0\)
\(\Rightarrow \left\{\begin{matrix} z^2+2z+2=0\\ z^2+2z+5=0\end{matrix}\right.\Rightarrow \) \(\left[\begin{matrix}z=-1+i\\z=-1-i\\z=-1+2i\\z=-1-2i\end{matrix}\right.\)
bạn giỏi thật