Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

giải pt ta có
\(\begin{cases}z=2+\sqrt{5i}\\z=2-\sqrt{5}i\end{cases}\)
===> 2 điểm M,N lần lượt là M( 2, \(\sqrt{5}\)) VÀ N(2,-\(\sqrt{5}\))
MN=\(\sqrt{\left(2-2\right)^2+\left(-\sqrt{5}-\sqrt{5}\right)^2}\)=2\(\sqrt{5}\)

Đáp án B
z 2 + 6 z + 13 = 0 ⇔ z = − 3 ± 2 i ⇒ z 1 = − 3 − 2 i z 2 = − 3 + 2 i w = z 1 + 2 z 2 = − 9 + 2 i

Đáp án B
z 2 + 6 z + 13 = 0 ⇔ z = − 3 ± 2 i ⇒ z 1 = − 3 − 2 i z 2 = − 3 + 2 i w = z 1 + 2 z 2 = − 9 + 2 i

Đáp án D.
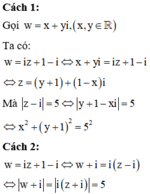
Do đó, điểm biểu diễn số phức z nằm trên đường tròn tâm I(0;-1) bán kính r = 5
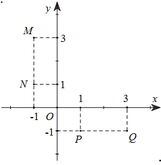

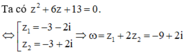
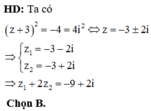
 bit lm bài này k giup tui
bit lm bài này k giup tui
Đáp án B