Câu 5: Nối hai cực của máy phát điện xoay chiều với một bóng đèn. Khi quay nam châm của máy phát thì trong cuộn dây của nó xuất hiện dòng điện xoay chiều vì:
A. Từ trường trong lòng cuộn dây luôn tăng
B. Số đường sức từ qua tiết diện S của cuộn dây luôn tăng
C. Từ trường trong lòng cuộn dây không biến đổi
D. Số đường sức từ qua tiết diện S của cuộn dây luân phiên tăng giảm

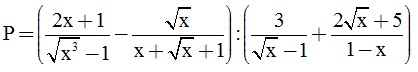
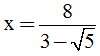 .
.
Câu 5: Nối hai cực của máy phát điện xoay chiều với một bóng đèn. Khi quay nam châm của máy phát thì trong cuộn dây của nó xuất hiện dòng điện xoay chiều vì:
A. Từ trường trong lòng cuộn dây luôn tăng
B. Số đường sức từ qua tiết diện S của cuộn dây luôn tăng
C. Từ trường trong lòng cuộn dây không biến đổi
D. Số đường sức từ qua tiết diện S của cuộn dây luân phiên tăng giảm
D vì
Nối hai cực của máy phát điện xoay chiều với một bóng đèn. Khi quay nam châm của máy phát thì trong cuộn dây của nó xuất hiện dòng điện cảm ứng xoay chiều vì: số đường sức từ qua tiết diện S của cuộn dây luân phiên tăng giảm.
Câu 5: Nối hai cực của máy phát điện xoay chiều với một bóng đèn. Khi quay nam châm của máy phát thì trong cuộn dây của nó xuất hiện dòng điện xoay chiều vì:
A. Từ trường trong lòng cuộn dây luôn tăng
B. Số đường sức từ qua tiết diện S của cuộn dây luôn tăng
C. Từ trường trong lòng cuộn dây không biến đổi
D. Số đường sức từ qua tiết diện S của cuộn dây luân phiên tăng giảm