hinh thuc tieng anh la gi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a. $(3x-1)^{10}=(3x-1)^{20}$
$(3x-1)^{20}-(3x-1)^{10}=0$
$(3x-1)^{10}[(3x-1)^{10}-1]=0$
$\Rightarrow (3x-1)^{10}=0$ hoặc $(3x-1)^{10}=1$
Nếu $(3x-1)^{10}=0$
$\Rightarrow 3x-1=0$
$\Rightarrow x=\frac{1}{3}$
Nếu $(3x-1)^{10}-1=0$
$\Rightarrow 3x-1=1$ hoặc $3x-1=-1$
$\Rightarrow x=\frac{2}{3}$ hoặc $x=0$
b
$x(6-x)^{2003}=(6-x)^{2003}$
$x(6-x)^{2003}-(6-x)^{2003}=0$
$(6-x)^{2003}(x-1)=0$
$\Rightarrow (6-x)^{2003}=0$ hoặc $x-1=0$
$\Rightarrow x=6$ hoặc $x=1$
c.
$5^x+5^{x+2}=650$
$5^x(1+5^2)=650$
$5^x.26=650$
$5^x=25=5^2$
$\Rightarrow x=2$
Bài 2:
a. Trùng với câu c bài 1
b.
$3^2.3^n=3^5$
$3^{n+2}=3^5$
$\Rightarrow n+2=5$
$\Rightarrow n=3$
c.
$(2^2:4).2^n=4$
$1.2^n=4=2^2$
$2^n=2^2$
$\Rightarrow n=2$

Lời giải:
$3A=1.2(3-0)+2.3(4-1)+3.4(5-2)+....+2020.2021(2022-2019)$
$=(1.2.3+2.3.4+3.4.5+....+2020.2021.2022)-(0.1.2+1.2.3+2.3.4+....+2019.2020.2021)$
$=2020.2021.2022$
$\Rightarrow A=\frac{2020.2021.2022}{3}$

Bạn nên tách lẻ từng bài từng post ra để khả năng nhận được sự trợ giúp cao hơn nhé. Đăng quá nhiều bài trong 1 post (nhất là bài hình) khiến mọi người nản, dễ bỏ qua bài của bạn hơn.

Gọi các phân số cần tìm là: \(\dfrac{a}{b}\) theo bài ra ta có:
\(\dfrac{a}{b}\) = \(\dfrac{a+2}{b\times2}\)
a.(b x 2) = (a + 2) x b
ab x 2 = ab + 2b
ab = 2b
a = 2
Ta có: \(\dfrac{2}{b}\) > \(\dfrac{1}{5}\) = \(\dfrac{2}{10}\)
⇒ b < 10 ⇒ b = 1; 2; 3; 4; 5; 6; 7; 8; 9
Vì \(\dfrac{2}{b}\) không phải là số tự nhiên nên b \(\in\) {3; 4; 5; 6; 7; 8; 9}
Bài 16:
\(\dfrac{1}{6}\) < \(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\) + \(\dfrac{1}{7^2}\) +...+ \(\dfrac{1}{100^2}\) < \(\dfrac{1}{4}\)
\(\dfrac{1}{5^2}\) < \(\dfrac{1}{4.5}\) = \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\)
\(\dfrac{1}{6^2}\) < \(\dfrac{1}{5.6}\) = \(\dfrac{1}{5}\) - \(\dfrac{1}{6}\)
............................
\(\dfrac{1}{100^2}\) < \(\dfrac{1}{99.100}\) = \(\dfrac{1}{99}\) - \(\dfrac{1}{100}\)
Cộng vế với vế ta có:
\(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\)+...+ \(\dfrac{1}{100^2}\) < \(\dfrac{1}{4}\) - \(\dfrac{1}{100}\) < \(\dfrac{1}{4}\) (1)
\(\dfrac{1}{5^2}\) > \(\dfrac{1}{5.6}\) = \(\dfrac{1}{5}\) - \(\dfrac{1}{6}\)
\(\dfrac{1}{6^2}\) > \(\dfrac{1}{6.7}\) = \(\dfrac{1}{6}\) - \(\dfrac{1}{7}\)
...............................
\(\dfrac{1}{100^2}\) > \(\dfrac{1}{100.101}\) = \(\dfrac{1}{100}\) - \(\dfrac{1}{101}\)
Cộng vế với vế ta có:
\(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\) + ... + \(\dfrac{1}{100^2}\) > \(\dfrac{1}{5}\) - \(\dfrac{1}{101}\)= \(\dfrac{96}{505}\) > \(\dfrac{96}{576}\) = \(\dfrac{1}{6}\) (2)
Kết hợp (1) và (2) ta có:
\(\dfrac{1}{6}\) < \(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\) +...+ \(\dfrac{1}{100^2}\) < \(\dfrac{1}{4}\) (đpcm)


\(A=\dfrac{1}{2^4}+\dfrac{1}{2^5}+\dfrac{1}{2^6}+\dots+\dfrac{1}{2^{100}}\)
\(2A=\dfrac{1}{2^3}+\dfrac{1}{2^4}+\dfrac{1}{2^5}+\dots+\dfrac{1}{2^{99}}\)
\(2A-A=\left(\dfrac{1}{2^3}+\dfrac{1}{2^4}+\dfrac{1}{2^5}+\dots+\dfrac{1}{2^{99}}\right)-\left(\dfrac{1}{2^4}+\dfrac{1}{2^5}+\dfrac{1}{2^6}+\dots+\dfrac{1}{2^{100}}\right)\)
\(A=\dfrac{1}{2^3}-\dfrac{1}{2^{100}}\)
\(A=\dfrac{2^{97}}{2^{100}}-\dfrac{1}{2^{100}}\)
\(A=\dfrac{2^{97}-1}{2^{100}}\)

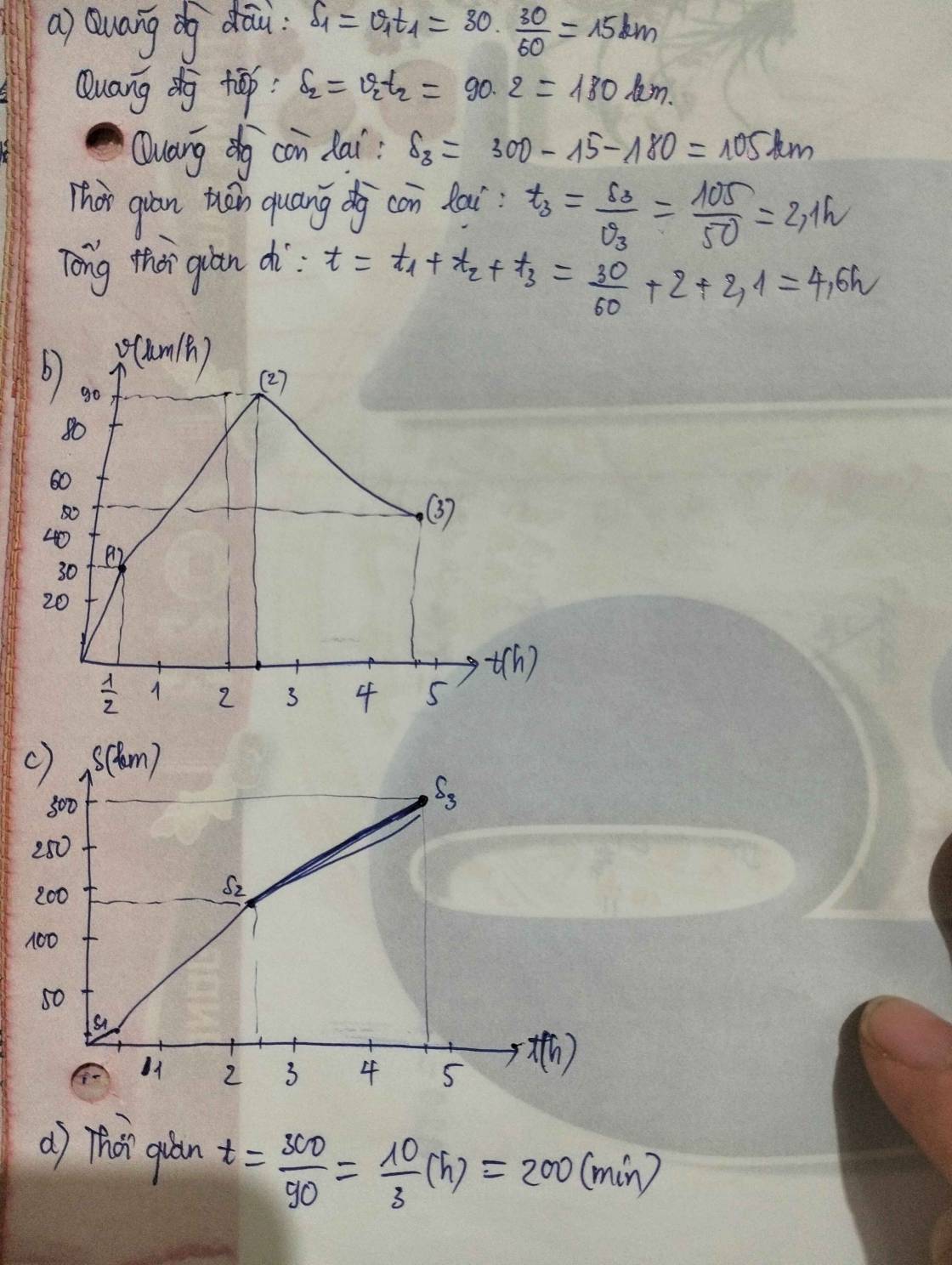


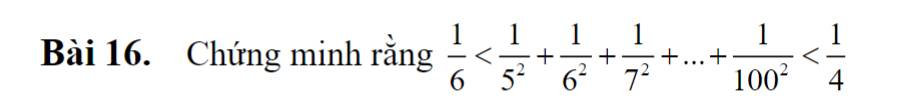 Cứu mình gấp ạ!!! Mình sắp thi rồi!!!
Cứu mình gấp ạ!!! Mình sắp thi rồi!!!
Hình thức là những gì làm thành bề ngoài của sự vật, chứa đựng hoặc biểu hiện nội dung. Hình thức là phạm trù chỉ phương thức tồn tại và phát triển của sự vật, là hệ thống các mối liên hệ tương đối bền vững giữa các yếu tố của sự vật đó.
Hình thức \(\rightarrow\) form (Tiếng Anh )