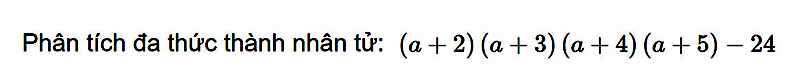
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\left(2x-5\right)\left(3x+b\right)=ax^2+bx+c\)
\(\Rightarrow6x^2+2bx-15x-5b=ax^2+bx+c\)
\(\Rightarrow6x^2+\left(2b-15\right)x-5b=ax^2+bx+c\)
\(\Rightarrow\left\{{}\begin{matrix}a=6\\2b-15=b\\-5b=c\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=6\\b=15\\c=-75\end{matrix}\right.\)
b) \(\left(ax+b\right)\left(x^2-x-1\right)=ax^3+cx^2-1\)
\(\Rightarrow ax^3-ax^2-ax+bx^2-bx-b=ax^3+cx^2-1\)
\(\Rightarrow ax^3-ax^2+bx^2-ax-bx-b=ax^3+cx^2-1\)
\(\Rightarrow ax^3+\left(b-a\right)x^2-\left(a+b\right)x-b=ax^3+cx^2-1\)
\(\Rightarrow\left\{{}\begin{matrix}b-a=c\\-\left(a+b\right)=0\\-b=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b-a=c\\a=-b\\b=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-1\\b=1\\c=2\end{matrix}\right.\)
c) \(ax\left(x-4\right)-b\left(x+6\right)+5=2x^2+5x\left(a-b\right)-6x+c\)
\(\Rightarrow ax^2-4ax-bx-6b+5=2x^2+\left(5a-5b\right)x-6x+c\)
\(\Rightarrow ax^2-\left(4a+b\right)x-\left(5a-5b\right)x-6b+5=2x^2-6x+c\)
\(\Rightarrow ax^2-\left(4a+b+5a-5b\right)x-6b+5=2x^2-6x+c\)
\(\Rightarrow ax^2-\left(9a-4b\right)x-6b+5=2x^2-6x+c\)
\(\Rightarrow\left\{{}\begin{matrix}a=2\\-\left(9a-4b\right)=-6\\-6b+5=c\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=2\\b=\dfrac{9a-6}{4}\\c=-6b+5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=2\\b=3\\c=-13\end{matrix}\right.\)

Lời giải:
a. Để $(1;-2)$ là nghiệm của PT đã cho thì:
$m.1+(-2)=-2$
$\Leftrightarrow m-2=-2$
$\Leftrightarrow m=0$
b.
Với $m=0$ thì PT trở thành: $0.x+y=-2$
Vì $0x=0,\forall x\in\mathbb{R}$
$\Rightarrow y=-2$
Vậy PT có nghiệm tổng quát $(x;-2)$ với $x\in\mathbb{R}$ tùy ý.

Giải:
+ Xét hạng tử thứ nhất là: 5\(x^3\) vậy hạng tử này có bậc là 3
+ Xét hạng tử thứ hai là: \(xy^2z^3\)
\(x\) có bậc là 1
y2 có bậc là 2
z3 có bậc là 3
Vậy hạng tử \(xy^2z^3\) có bậc là: 1 + 2 + 3 = 6
+ Bậc của hạng tử \(xy^2z^3\) lớn hơn bậc của hạng tử - 5\(x^3\) nên đó là bậc của đa thức vì vậy bậc của đa thức là 6

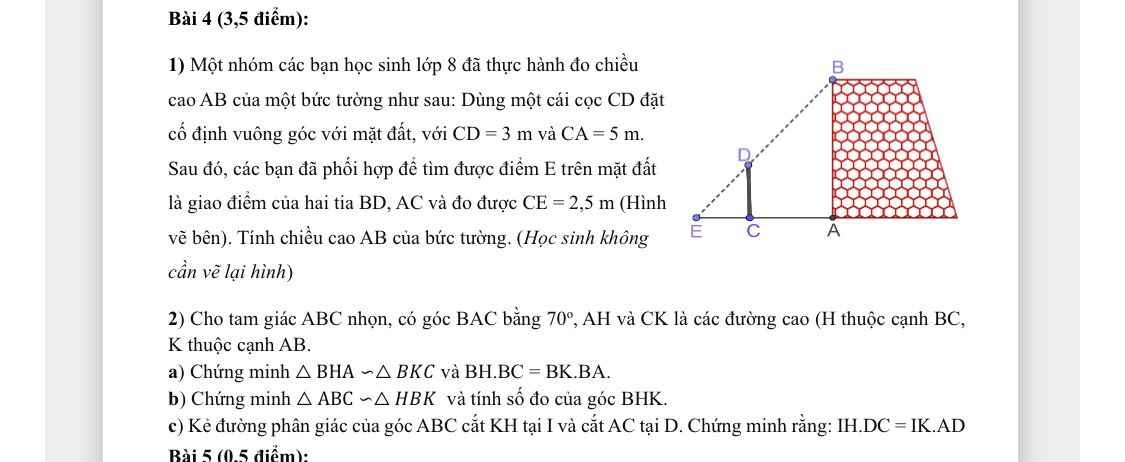
2:
a: Xét ΔBHA vuông tại H và ΔBKC vuông tại K có
\(\widehat{HBA}\) chung
Do đó: ΔBHA~ΔBKC
=>\(\dfrac{BH}{BK}=\dfrac{BA}{BC}\)(2)
=>\(\dfrac{BH}{BA}=\dfrac{BK}{BC}\)
=>\(BH\cdot BC=BK\cdot BA\)
b: Xét ΔBHK và ΔBAC có
\(\dfrac{BH}{BA}=\dfrac{BK}{BC}\)
\(\widehat{HBK}\) chung
Do đó: ΔBHK~ΔBAC
=>\(\widehat{BHK}=\widehat{BAC}=70^0\)
c: Xét ΔBKH có BI là phân giác
nên \(\dfrac{IH}{IK}=\dfrac{BH}{BK}\left(1\right)\)
Xét ΔBAC có BD là phân giác
nên \(\dfrac{DA}{DC}=\dfrac{BA}{BC}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{IH}{IK}=\dfrac{DA}{DC}\)
=>\(IH\cdot DC=DA\cdot IK\)

Bài 1
\(1,\left(x+1\right)^3-\left(x-4\right)\left(x+4\right)-x^3=x^3+3x^2+3x+1-x^2+16-x^3=2x^2+3x+17\)
2, \(\left(x+2\right)^3-x\left(x+3\right)\left(x-3\right)-12x^2-8=x^3+6x^2+12x+8-x\left(x^2-9\right)-12x^2-8\)
\(=x^3+6x^2+12x+8-x^3+9x-12x^2-8=-6x^2+21x\)
3, \(\left(x-2\right)^3-x\left(x-2\right)\left(x+2\right)+6x\left(x-3\right)\)
\(=x^3-6x^2+12x-8-x\left(x^2-4\right)+6x^2-18x\)
\(=x^3+12x-8-x^3+4x-18x=2x=8\)
4, \(x\left(x-5\right)\left(x+5\right)-\left(x-5\right)^3+100x\)
\(=\left(x-5\right)\left[x^2+5x-\left(x-5\right)^2\right]+100x\)
\(=\left(x-5\right)\left(x^2+5x-x^2+10x-25\right)+100x=\left(x-5\right)\left(15x-25\right)+100x\)
\(=15x^2-100x+125+100x=15x^2+125\)
5, \(\left(x-3y\right)^3-\left(x-2y\right)\left(2y+x\right)=x^3-9x^2y+27xy^2-27y^3-x^2+4y^2\)
6, \(\left(-x-2y\right)^3+x\left(2y-x\right)\left(x+2y\right)=-\left(x+2y\right)^3+x\left(2y-x\right)\left(x+2y\right)\)
\(=\left(x+2y\right)\left[-\left(x+2y\right)^2+2xy-x^2\right]=\left(x+2y\right)\left(-x^2-4xy-4y^2+2xy-x^2\right)=\left(x+2y\right)\left(-2x^2-2xy-4y^2\right)\)
\(=\left(x+2y\right)\left(-2x^2-2xy-4y^2\right)=-2x^3-2x^2y-4xy^2-4x^2y+4xy^2-8y^3=-2x^3-6x^2y-8y^3\)
7, \(-\left(2x-y\right)^3-x\left(2x-y\right)^2-y^3\)
\(=-\left(8x^3-12x^2y+6xy^2-y^3\right)-x\left(4x^2-4xy+y^2\right)-y^3=-12x^3+16x^2y-7xy^2\)
8, \(-x\left(x-y\right)^2+\left(x-y\right)^3+y^2\left(y-2x\right)\)
\(=-x\left(x^2-2xy+y^2\right)+x^3-3x^2y+3xy^2-y^3+y^3-2xy^2=-x^2y\)
Bài 6:
1)
\(8x^3-12x^2+6x-1=0\\ \Leftrightarrow\left(2x-1\right)^3=0\\ \Leftrightarrow2x-1=0\\ \Leftrightarrow2x=1\\ \Leftrightarrow x=\dfrac{1}{2}\)
2)
\(x^3-6x^2+12x-8=0\\ \Leftrightarrow\left(x-2\right)^3=0\\ \Leftrightarrow x-2=0\\ \Leftrightarrow x=2\)
3)
\(x^2-8x+16=5\left(4-x\right)^3\\ \Leftrightarrow\left(x-4\right)^2-5\left(4-x\right)^3=0\\ \Leftrightarrow\left(4-x\right)^2-5\left(4-x\right)^3=0\\ \Leftrightarrow\left(4-x\right)^2\left[1-5\left(4-x\right)\right]=0\\ \Leftrightarrow\left(4-x\right)^2\left(5x-19\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=4\\x=\dfrac{19}{5}\end{matrix}\right.\)
4)
\(\left(2-x\right)^3=6x\left(x-2\right)\\ \Leftrightarrow\left(2-x\right)^3-6x\left(x-2\right)=0\\ \Leftrightarrow\left(2-x\right)^3+6x\left(2-x\right)=0\\ \Leftrightarrow\left(2-x\right)\left[\left(2-x\right)^2+6x\right]=0\\ \Leftrightarrow\left(2-x\right)\left(4-4x+x^2+6x\right)=0\\ \Leftrightarrow\left(2-x\right)\left(x^2+2x+4\right)=0\\ \Leftrightarrow2-x=0\\ \Leftrightarrow x=2\)
(vì x^2+2x+4=x^2+2x+1+3=(x+1)^2+3>0)

\(\left[a+\left(b+c\right)\right]^2\\=a^2+2a\left(b+c\right)+\left(b+c\right)^2\\ =a^2+2ab+2ac+\left(b^2+2bc+c^2\right)\\ =a^2+b^2+c^2+2ab+2ac+2bc\)

a: ΔABC cân tại A
mà AD là đường cao
nên D là trung điểm của BC
ΔADB vuông tại D
=>\(DA^2+DB^2=AB^2\)
=>\(DB=\sqrt{5^2-4^2}=3\left(cm\right)\)
b: Xét ΔHDB vuông tại D và ΔHEA vuông tại E có
\(\widehat{DHB}=\widehat{EHA}\)(hai góc đối đỉnh)
Do đó: ΔHDB~ΔHEA
=>\(\dfrac{HD}{HE}=\dfrac{HB}{HA}\)
=>\(HD\cdot HA=HB\cdot HE\)
 ai biết làm giúp e vs
ai biết làm giúp e vs 
\(\left(a+2\right)\left(a+3\right)\left(a+4\right)\left(a+5\right)-24\)
\(=\left(a^2+7a+10\right)\left(a^2+7a+12\right)-24\)
Đặt a^2 + 7a = t
\(\left(t+10\right)\left(t+12\right)-24=t^2+22t+120-24\)
\(=\left(t+6\right)\left(t+16\right)\)
\(\Rightarrow\left(a^2+7a+6\right)\left(a^2+7a+16\right)=\left(a+1\right)\left(a+6\right)\left(a^2+7a+16\right)\)