Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 3:
a: Xét ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
Do đó: ΔAIB=ΔCID
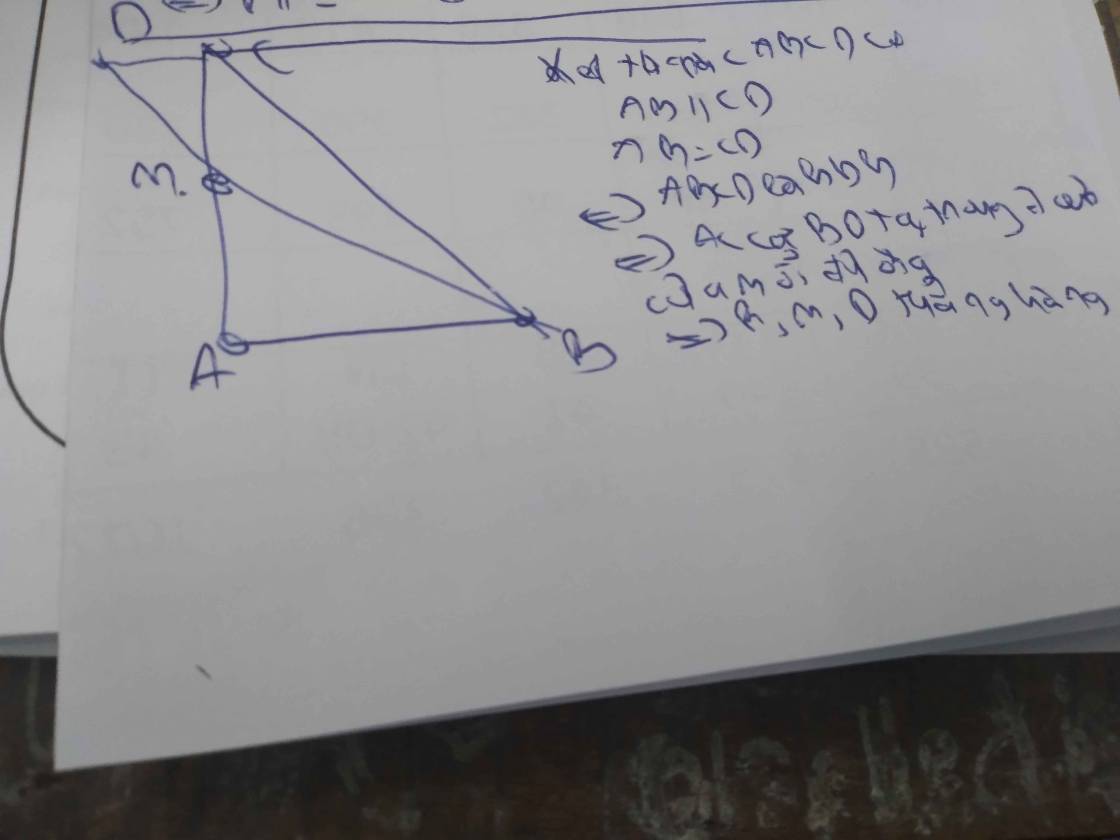
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Suy ra: AD//BC va AD=BC
Bài 6:
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=BD
Do đó: ΔEBC=ΔDCB
Suy ra: góc OBC=góc OCB
=>ΔOBC cân tại O
=>OB=OC
=>OE=OD
=>ΔOED cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC

ta có:AE vuông góc với AC ;AB vuông góc với AF
suy ra: góc AEC=90độ;góc BAF=90đ
mà góc BAC+góc EAB= góc AEC=90đ
góc BAC+góc CAF=góc BAF=90đ
suy ra: góc EAB=góc CAF
xét tam giác AEBvà ACF có:
AE=AC
AB=AF
góc EAB= góc ACF (cmt)
suy ra tam giác AEB=ACF ( C.G.C)
suy ra EB= CF ( cạnh tương ứng)

Câu 1:
1. Vì P,QP,Q lần lượt là trung điểm của AB,ACAB,AC nên PQPQ là đường trung bình của tam giác ABCABC ứng với BCBC
⇒PQ=1BC=MC⇒PQ=1BC=MC và PQ∥BCPQ∥BC hay PQ∥MCPQ∥MC
Tứ giác PQCMPQCM có cặp cạnh đối PQPQ và MCMC vừa song song vừa bằng nhau nên PQCMPQCM là hình bình hành.
2.Vì tam giác ABCABC cân tại AA nên đường trung tuyến AMAM đồng thời là đường cao. Hay AM⊥BCAM⊥BC
Tứ giác NAMBNAMB có 2 đường chéo MN,ABMN,AB cắt nhau tại trung điểm PP của mỗi đường nên NAMBNAMB là hình bình hành.
Hình bình hành NAMBNAMB có 1 góc vuông (ˆAMBAMB^) nên NAMBNAMB là hình vuông.
⇒NB⊥BM⇒NB⊥BM hay NB⊥BCNB⊥BC (đpcm)
3.
Vì PQCMPQCM là hình bình hành nên PM∥QC;PM=QCPM∥QC;PM=QC. Mà P,M,NP,M,N thẳng hàng; PM=PNPM=PN nên PN∥QCPN∥QC và PN=QCPN=QC
Tứ giác PNQCPNQC có cặp cạnh đối PN,QCPN,QC song song và bằng nhau nên PNQCPNQC là hình bình hành.
Do đó PC∥QN(1)PC∥QN(1)
Mà PC∥QFPC∥QF (2)
Từ (1);(2)⇒Q,N,F(1);(2)⇒Q,N,F thẳng hàng (đpcm)
M là trung điểm của đoạn nào vậy bạn?