Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(\dfrac{2}{3}\right)^8:\left(\dfrac{4}{9}\right)^3\\ =\left[\left(\dfrac{2}{3}\right)^2\right]^4:\left(\dfrac{4}{9}\right)^3\\ =\left(\dfrac{4}{9}\right)^4:\left(\dfrac{4}{9}\right)^3\\ =\dfrac{4}{9}\)
\(27^3:3^2\\ =\left(3^3\right)^3:3^2\\ =3^9:3^2\\ =3^7\\ =2187\)
\(\left(-\dfrac{3}{5}\right)^4:\left(\dfrac{5}{2}\right)^4\\ =\left(-\dfrac{3}{5}:\dfrac{5}{2}\right)^4\\ =\left(-\dfrac{6}{25}\right)^4\)
\(\left(\dfrac{3}{5}\right)^{12}:\left(\dfrac{9}{25}\right)^5\\ =\left(\dfrac{3}{5}\right)^{12}:\left[\left(\dfrac{3}{5}\right)^2\right]^5\\ =\left(\dfrac{3}{5}\right)^{12}:\left(\dfrac{3}{5}\right)^{10}\\ =\left(\dfrac{3}{5}\right)^2\\ =\dfrac{9}{25}\)
\(\left(\dfrac{2}{3}\right)^8:\left(\dfrac{4}{9}\right)^3=\left(\dfrac{4}{9}\right)^4:\left(\dfrac{4}{9}\right)^3=\dfrac{4}{9}\)
\(27^3:3^2=3^9:3^2=3^7=2187\)

a) Ta có:
\(64^8=\left(2^6\right)^8=2^{6\cdot8}=2^{48}\)
\(16^{12}=\left(2^4\right)^{12}=2^{4\cdot12}=2^{48}\)
\(\Rightarrow64^8=16^{12}\)
b) Ta có:
\(\left(\dfrac{1}{16}\right)^{10}=\left[\left(\dfrac{1}{2}\right)^4\right]^{10}=\left(\dfrac{1}{2}\right)^{4\cdot10}=\left(\dfrac{1}{2}\right)^{40}\)
Mà: 50 > 40 => `(1/2)^50<(1/2)^40`
c) Ta có:
\(\left(\dfrac{9}{16}\right)^{100}=\left[\left(\dfrac{3}{4}\right)^2\right]^{100}=\left(\dfrac{3}{4}\right)^{200}\)
Mà: `3/4>2/3=>(3/4)^200>(2/3)^200`
\(^{^{ }}\)a,64^8=16^12
b,(1/16)^10<(1/2)^50
c,(2/3)^200>(9/16)^100
CỦA BẠN ĐÂY NẾU SAI THÌ CHO MÌNH XIN LỖI NHÉ

Để hộp quà đựng vừa quả bóng thì cạnh của hộp quà phải bằng đường kính của quả bóng.
Vậy cạnh của hình lập phương là : 10,5 cm
Thể tích tối thiểu của hình lập phương là:
10,5 x10,5 x10,5 = 1157,625 ( cm ^ 3)
Đáp số : 1157,625 cm ^3

a; 25 x 53 x \(\dfrac{1}{625}\) x 52
= 52 x 53 x \(\dfrac{1}{5^4}\) x 52
= 55 x \(\dfrac{1}{5^4}\) x 52
= 5 x 52
= 53
a)
\(25\cdot5^3\cdot\dfrac{1}{625}\cdot5^2\\ =\left(5^2\cdot5^3\cdot5^2\right)\cdot\dfrac{1}{625}\\ =5^7\cdot\dfrac{1}{5^4}\\ =5^3\)
b)
\(5^2\cdot3^5\cdot\left(\dfrac{3}{5}\right)^2\\ =5^2\cdot3^5\cdot\dfrac{3^2}{5^2}\\ =3^5\cdot3^2\\ =3^7\)
c)
\(\left(-\dfrac{1}{7}\right)^4\cdot49^2\\ =\dfrac{\left(-1\right)^4}{7^4}\cdot\left(7^2\right)^2\\ =\dfrac{1}{7^4}\cdot7^4\\ =1\)
d)
\(\left(\dfrac{1}{16}\right)^2:\left(\dfrac{1}{2}\right)^4\cdot\left(-\dfrac{1}{8}\right)^3\\ =\left[\left(\dfrac{1}{2}\right)^4\right]^2:\left(\dfrac{1}{2}\right)^4\cdot\left[\left(-\dfrac{1}{2}\right)^3\right]^3\\ =\left(\dfrac{1}{2}\right)^8:\left(\dfrac{1}{2}\right)^4\cdot\left(-\dfrac{1}{2}\right)^9\\ =\left(\dfrac{1}{2}\right)^4\cdot\left(-\dfrac{1}{2}\right)^9\\ =\left(\dfrac{1}{2}\right)^4\cdot-\left(\dfrac{1}{2}\right)^9\\ =-\left(\dfrac{1}{2}\right)^{13}\)

a; \(x\) : (- \(\dfrac{1}{3}\))3 = \(\dfrac{1}{9}\)
\(x\) : (\(-\dfrac{1}{27}\)) = \(\dfrac{1}{9}\)
\(x\) = \(\dfrac{1}{9}\) x (- \(\dfrac{1}{27}\))
\(x\) = - \(\dfrac{1}{243}\)
Vậy \(x\) = - \(\dfrac{1}{243}\)
b; (\(\dfrac{4}{5}\))5 x \(x\) = (\(\dfrac{4}{5}\))7
\(x\) = (\(\dfrac{4}{5}\))7 : (\(\dfrac{4}{5}\))5
\(x\) = \(\dfrac{4^7}{5^7}\) : \(\dfrac{4^5}{5^5}\)
\(x\) = \(\dfrac{4^7}{5^7}\) x \(\dfrac{5^5}{4^5}\)
\(x\) = \(\dfrac{4^2}{5^2}\)
\(x\) = \(\dfrac{16}{25}\)
Vậy \(x\) = \(\dfrac{16}{25}\)

a; 5 - (- \(\dfrac{5}{11}\) ) + (\(\dfrac{1}{3}\))2 : 3
= 5 + \(\dfrac{5}{11}\) + \(\dfrac{1}{9}\) : 3
= \(\dfrac{55}{11}\) + \(\dfrac{5}{11}\) + \(\dfrac{1}{9}\) x \(\dfrac{1}{3}\)
= \(\dfrac{55}{11}\) + \(\dfrac{5}{11}\) + \(\dfrac{1}{27}\)
= \(\dfrac{60}{11}\) + \(\dfrac{1}{27}\)
= \(\dfrac{1620}{297}\) + \(\dfrac{11}{297}\)
= \(\dfrac{1631}{297}\)
b; 23 + 3 x (\(\dfrac{1}{2}\))0 + (- 2)2 : \(\dfrac{1}{2}\)
= 8 + 3 x 1 + 4 : \(\dfrac{1}{2}\)
= 8 + 3 + 4 x \(\dfrac{2}{1}\)
= 8 + 3 + 8
= 11 + 8
= 19

a: ΔABC cân tại A
mà AD là đường cao
nên D là trung điểm của BC
ΔADB vuông tại D
=>\(DA^2+DB^2=AB^2\)
=>\(DB=\sqrt{5^2-4^2}=3\left(cm\right)\)
b: Xét ΔHDB vuông tại D và ΔHEA vuông tại E có
\(\widehat{DHB}=\widehat{EHA}\)(hai góc đối đỉnh)
Do đó: ΔHDB~ΔHEA
=>\(\dfrac{HD}{HE}=\dfrac{HB}{HA}\)
=>\(HD\cdot HA=HB\cdot HE\)
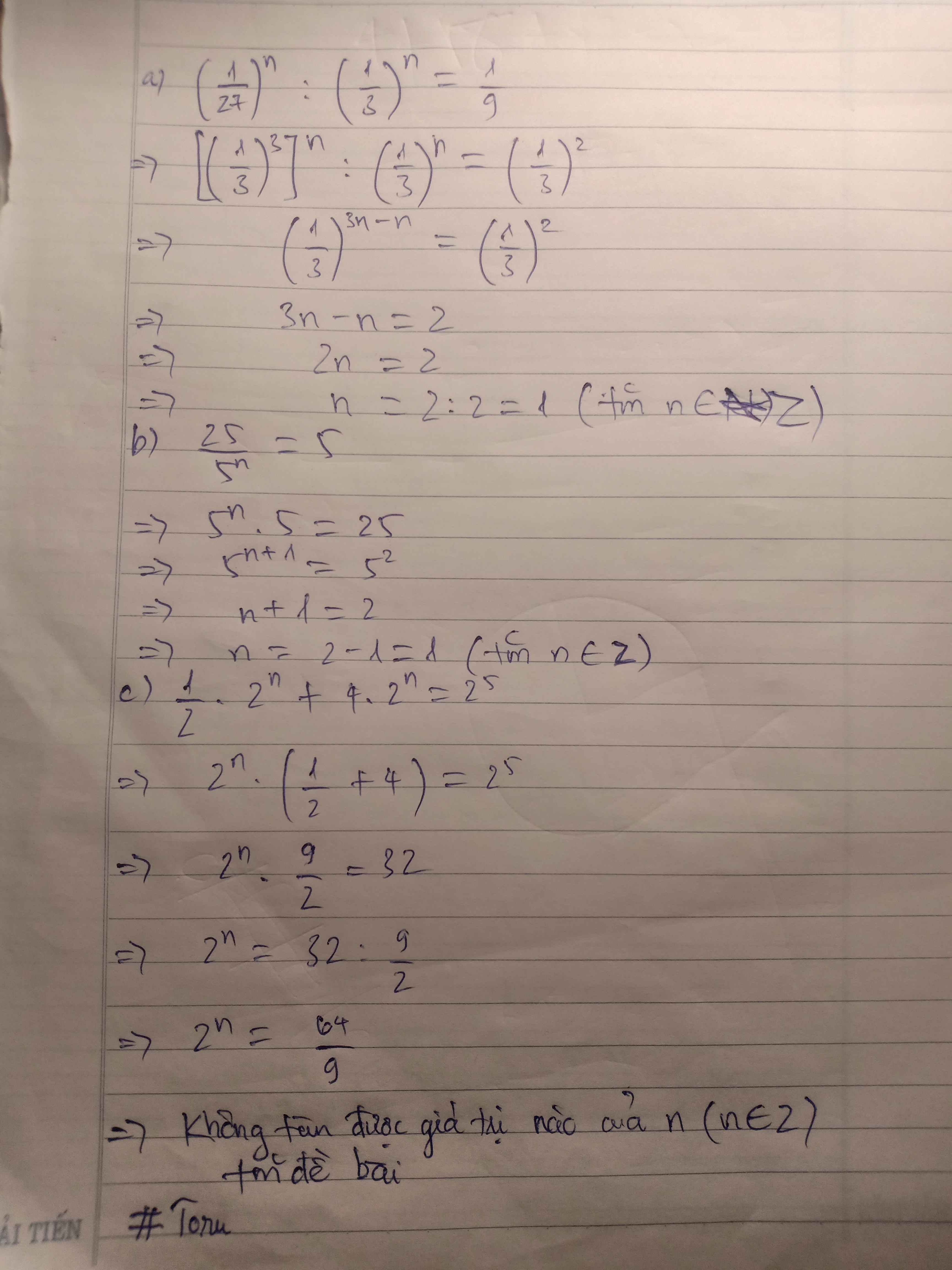

đâu
Olm chào em,hiện tại yêu cầu của em chưa cụ thể, vậy em vui lòng đăng lại câu hỏi để được sự trợ giúp tốt nhất từ olm cho tài khoản vip em nhé.