
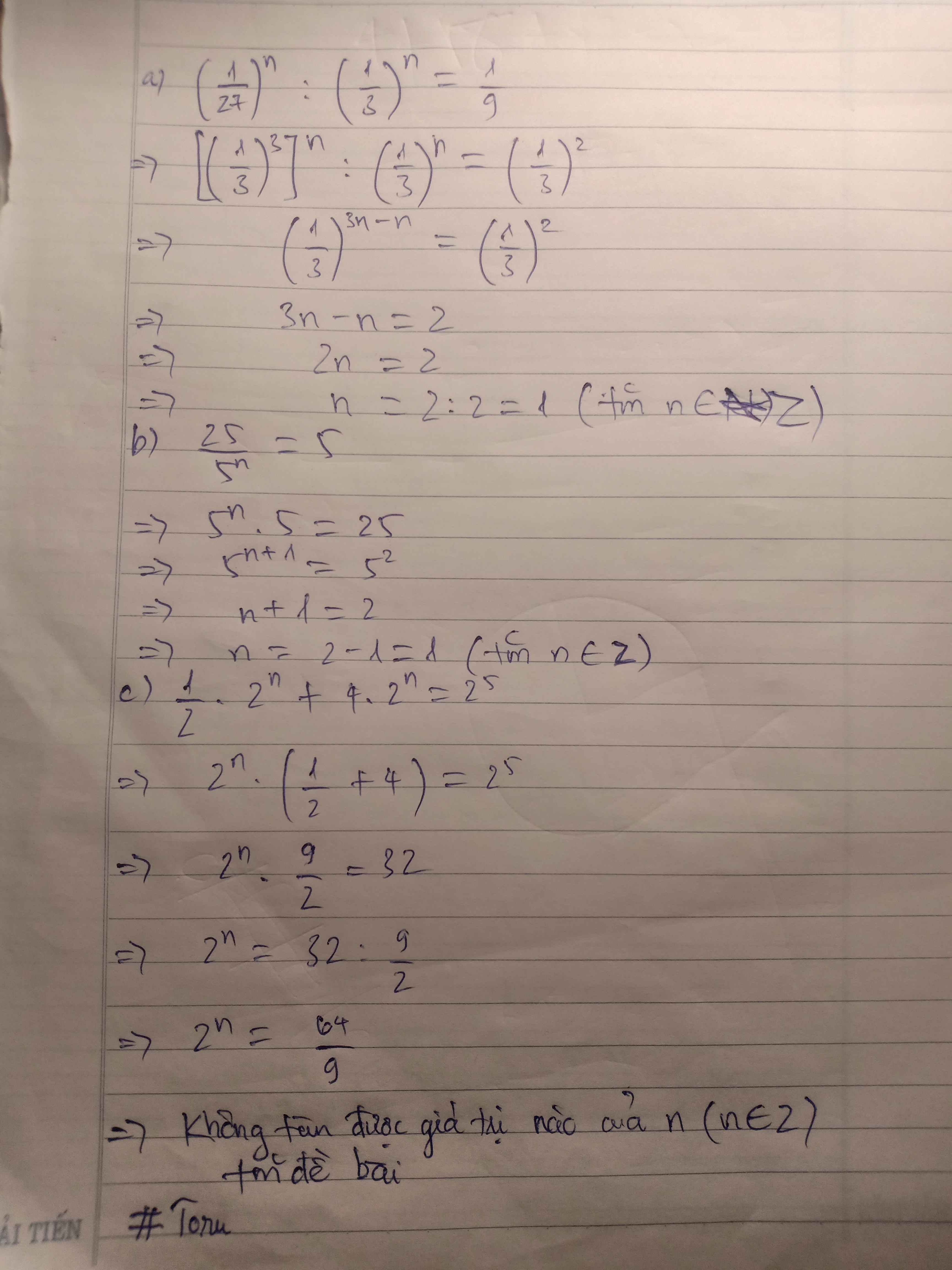
a, ( 1/27)\(^n\) : ( 1/3) Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời. Bài 1: a, \(\left(x-2\right)^2=9\) \(\Rightarrow x-2\in\left\{-3;3\right\}\Rightarrow x\in\left\{-1;5\right\}\) b, \(\left(3x-1\right)^3=-8\) \(\Rightarrow3x-1=-2\Rightarrow3x=-1\) \(\Rightarrow x=-\dfrac{1}{3}\) c, \(\left(x+\dfrac{1}{2}\right)^2=\dfrac{1}{16}\) \(\Rightarrow x+\dfrac{1}{2}\in\left\{-\dfrac{1}{4};\dfrac{1}{4}\right\}\) \(\Rightarrow x\in\left\{-\dfrac{3}{4};-\dfrac{1}{4}\right\}\) d, \(\left(\dfrac{2}{3}\right)^x=\dfrac{4}{9}\) \(\Rightarrow\left(\dfrac{2}{3}\right)^x=\left(\dfrac{2}{3}\right)^2\) Vì \(\dfrac{2}{3}\ne\pm1;\dfrac{2}{3}\ne0\) nên \(x=2\) e, \(\left(\dfrac{1}{2}\right)^{x-1}=\dfrac{1}{16}\) \(\Rightarrow\left(\dfrac{1}{2}\right)^{x-1}=\left(\dfrac{1}{2}\right)^4\) Vì \(\dfrac{1}{2}\ne\pm1;\dfrac{1}{2}\ne0\) nên \(x-1=4\Rightarrow x=5\) a. Vì A thuộc Z \(\Rightarrow x-2\in\left\{-5;-1;1;5\right\}\) \(\Rightarrow x\in\left\{-3;1;3;7\right\}\)( tm x thuộc Z ) b. Ta có : \(B=\frac{x+2}{x-3}=\frac{x-3+5}{x-3}=1+\frac{5}{x-3}\) Vì B thuộc Z nên 5 / x - 3 thuộc Z \(\Rightarrow x-3\in\left\{-5;-1;1;5\right\}\) \(\Rightarrow x\in\left\{-2;2;4;8\right\}\)( tm x thuộc Z ) c. Ta có : \(C=\frac{x^2-x}{x+1}=\frac{x^2+x-2x+2-2}{x+1}=\frac{x\left(x+1\right)-2x+2-2}{x+1}\) \(=x-2-\frac{2}{x+1}\) Vi C thuộc Z nên 2 / x + 1 thuộc Z \(\Rightarrow x+1\in\left\{-2;-1;1;2\right\}\) \(\Rightarrow x\in\left\{-3;-2;0;1\right\}\) ( tm x thuộc Z ) \(4)\) \(\dfrac{-\left(-x\right)}{5}-\dfrac{2}{10}=\dfrac{1}{-5}-\dfrac{7}{50}\) \(\Leftrightarrow\dfrac{x}{5}-\dfrac{2}{10}=\dfrac{1}{-5}-\dfrac{7}{50}\) \(\dfrac{2x}{10}-\dfrac{2}{10}=\dfrac{-10}{50}-\dfrac{7}{50}\) \(\Leftrightarrow\dfrac{2x-2}{10}=\dfrac{-10-7}{50}\) \(\dfrac{2x-2}{10}=\dfrac{-17}{50}\) \(\Leftrightarrow50\left(2x-2\right)=-17.10\) \(100x-100=-170\) \(100x=-170+100=-70\) \(x=-70:100=\dfrac{-7}{10}\) \(\dfrac{x+1}{5}=\dfrac{7}{x-1}\) \(\left(x+1\right)\left(x-1\right)5.7\) \(x\left(x-1\right)+1\left(x-1\right)=35\) \(x^2-x+x-1=35\) \(x^2-1=35\) \(x^2=36\) \(\Leftrightarrow x=\left\{\pm6\right\}\) bạn có thể giải đc các bài còn lại k ? K phải mk ép bạn đâu nhưng nếu bạn lm đc thì giúp mk nha a) 32 . 3n = 35 => 3n = 35 : 32 => 3n = 33 => n = 3 b) (22 : 4) . 2n = 4 => (4 : 4) . 2n = 4 => 2n = 4 => 2n = 22 => n = 2 c) \(\frac{1}{9}.3^4.3^n=3^7\) \(\Rightarrow3^{-2}.3^4.3^n=3^7\) \(\Rightarrow3^{-2+4+n}=3^7\) \(\Rightarrow3^{2+n}=3^7\) \(\Rightarrow2+n=7\) \(\Rightarrow n=5\) d) \(\frac{1}{9}.27^n=3^n\) \(\Rightarrow3^{-2}.3^{3n}=n\) \(\Rightarrow3^{-2+3n}=n\) \(\Rightarrow-2+3n=n\) \(\Rightarrow2n=2\) \(\Rightarrow n=1\) BÀi 1 Để A \(\in\) Z =>\(\left(n+2\right)⋮\left(n-5\right)\) =>\([\left(n-5\right)+7]⋮\left(n-5\right)\) =>\(7⋮\left(n-5\right)\) =>\(n-5\in\left\{1;7;-1;-7\right\}\) =>\(n\in\left\{6;13;4;-2\right\}\) Vậy \(n\in\left\{6;13;4;-2\right\}\) Ta có:\(\dfrac{x}{-12}=\dfrac{-3}{x}\) \(\Rightarrow x.x=-3.\left(-12\right)\) \(x^2=36\) Vì \(x\in Z\)\(\Rightarrow x=\pm6\) bài 4 dễ mà , bạn làm xong rồi gửi cho mik , đễ mik xem có đúng k nhé Ta có: 1/3 + −2/5+ 1/6 + −1/5 ≤ x < −3/4+2/7+-1/4+3/5+5/7 ⇒10-12+5-6/30≤ x< -105+40-35+84+100/140 ⇒-3/30≤ x <84/140 ⇒-0,1≤ x < 0,6 ⇒x=0 \(.2.\) \(a.\) \(2x+\dfrac{1}{2}=-\dfrac{5}{3}\) \(\Rightarrow2x=-\dfrac{5}{3}-\dfrac{1}{2}=-\dfrac{13}{6}\) \(\Rightarrow x=-\dfrac{13}{6}:2=-\dfrac{13}{12}\) Vậy : \(x=-\dfrac{13}{12}\) \(b.\) \(\dfrac{1}{7}-\dfrac{3}{5}x=\dfrac{3}{5}\) \(\Rightarrow\dfrac{3}{5}x=\dfrac{1}{7}-\dfrac{3}{5}=-\dfrac{16}{35}\) \(\Rightarrow x=-\dfrac{16}{35}:\dfrac{3}{5}=-\dfrac{16}{21}\) Vậy : \(x=-\dfrac{16}{21}\) \(c.\) \(\dfrac{3}{4}x+\dfrac{1}{2}=-\dfrac{3}{5}\) \(\Rightarrow\dfrac{3}{4}x=-\dfrac{3}{5}-\dfrac{1}{2}=-\dfrac{11}{10}\) \(\Rightarrow x=-\dfrac{11}{10}:\dfrac{3}{4}=-\dfrac{22}{15}\) Vậy : \(x=-\dfrac{22}{15}\) \(d.\) \(-\dfrac{2}{15}-x=-\dfrac{3}{10}\) \(\Rightarrow x=-\dfrac{2}{15}-\left(-\dfrac{3}{10}\right)=\dfrac{1}{6}\) Vậy : \(x=\dfrac{1}{6}\) Bài 1: Ta có: \(x^2+3x+9⋮x+3\) \(\Rightarrow x\left(x+3\right)+9⋮x+3\) Vì \(x\left(x+3\right)⋮x+3\) nên \(9⋮x+3\) \(\Rightarrow x+3\inƯ\left(9\right)\) \(\Rightarrow x+3\in\left\{\pm1;\pm3;\pm9\right\}\) \(\Rightarrow x\in\left\{-2;-4;0;-6;6;-12\right\}\) Vậy \(x\in\left\{-2;-4;0;\pm6;-12\right\}\). Bài 2: a) Để \(\dfrac{n+5}{n-2}\in Z\) thì \(n+5⋮n-2\) \(\Rightarrow\left(n-2\right)+7⋮n-2\) mà \(n-2⋮n-2\Rightarrow7⋮n-2\) \(\Rightarrow n-2\inƯ\left(7\right)\) \(\Rightarrow n-2\in\left\{\pm1;\pm7\right\}\) ... b) Tương tự bài a.
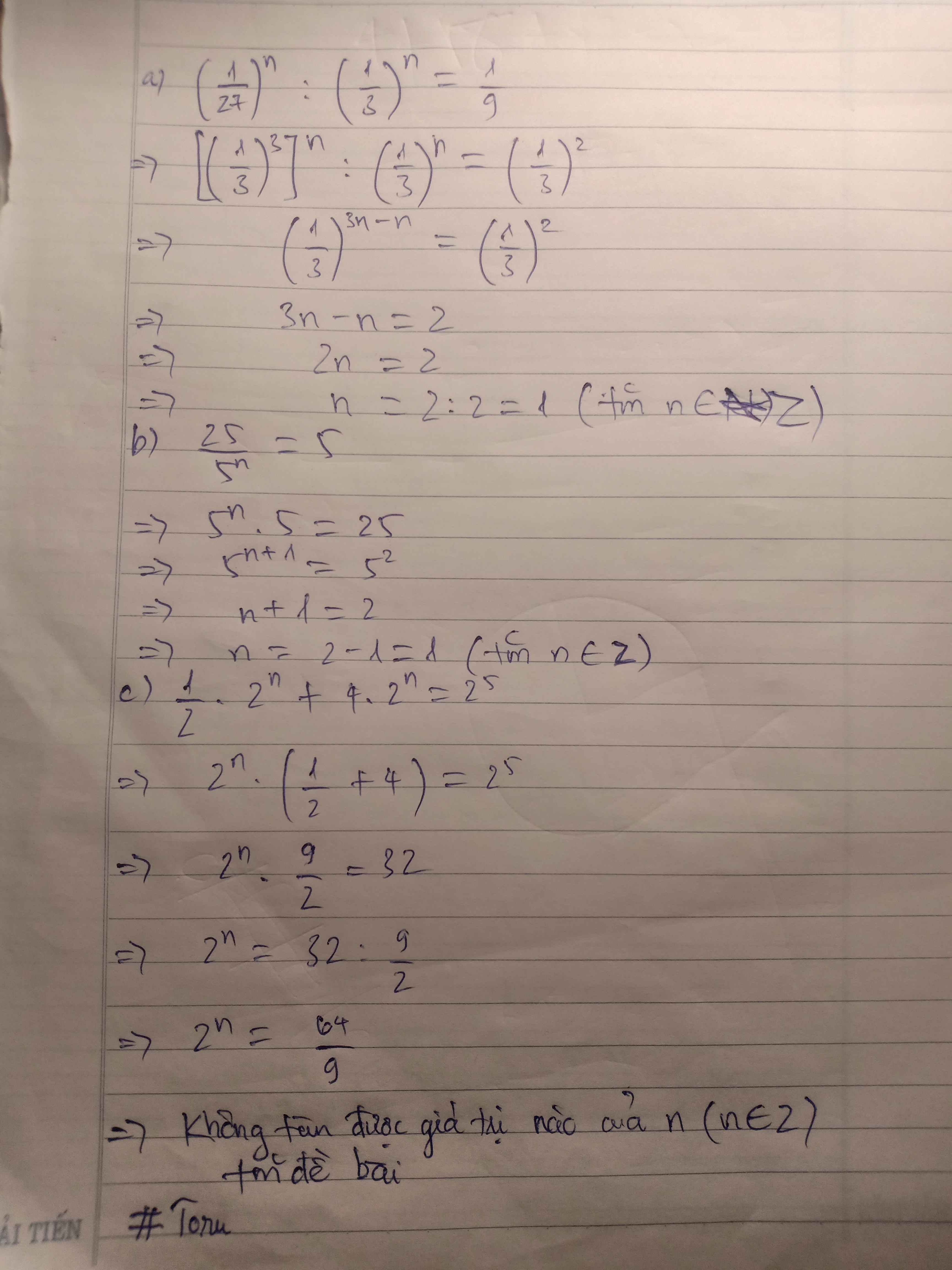






![]()


