Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Quy luật: Hiệu của số lớn hơn trừ cho số nhỏ hơn trong mổi ô chính là kết quả của ô màu vàng đối diện
17-13=4
15-6=9
14-8=6
19-12=7
23-15=8
27-25=2
23-18=5
Suy ra: 12-x=3
=> x=12-3=9
Đáp án C
Giải thích: Mỗi số trong hình tam giác màu vàng bằng số lớn hơn của hình bình hành đối diện trừ đi số bé hơn ở hình bình hành đối diện.
=> ? - 12 = 3 hoặc 12 - ? = 3
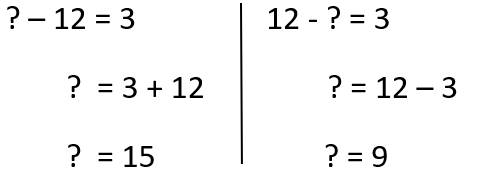
=> Đáp án là 15 hoặc 9
Đáp án: c
Bổ sung: Đáp án cũng có thể là 15

Ta có các quy luật sau:
\(\left(1+3\right)-2=2\)
\(\left(2+2\right)-3=1\)
\(\left(5+5\right)-6=4\)
Vậy dòng cuối là:
\(\left(5+9\right)-5=9\)
Số điền vào là 9
(Quy luật: lấy 2 số phía dưới cộng với nhau rồi trừ cho số phía trên sẽ ra được số ở giữa)

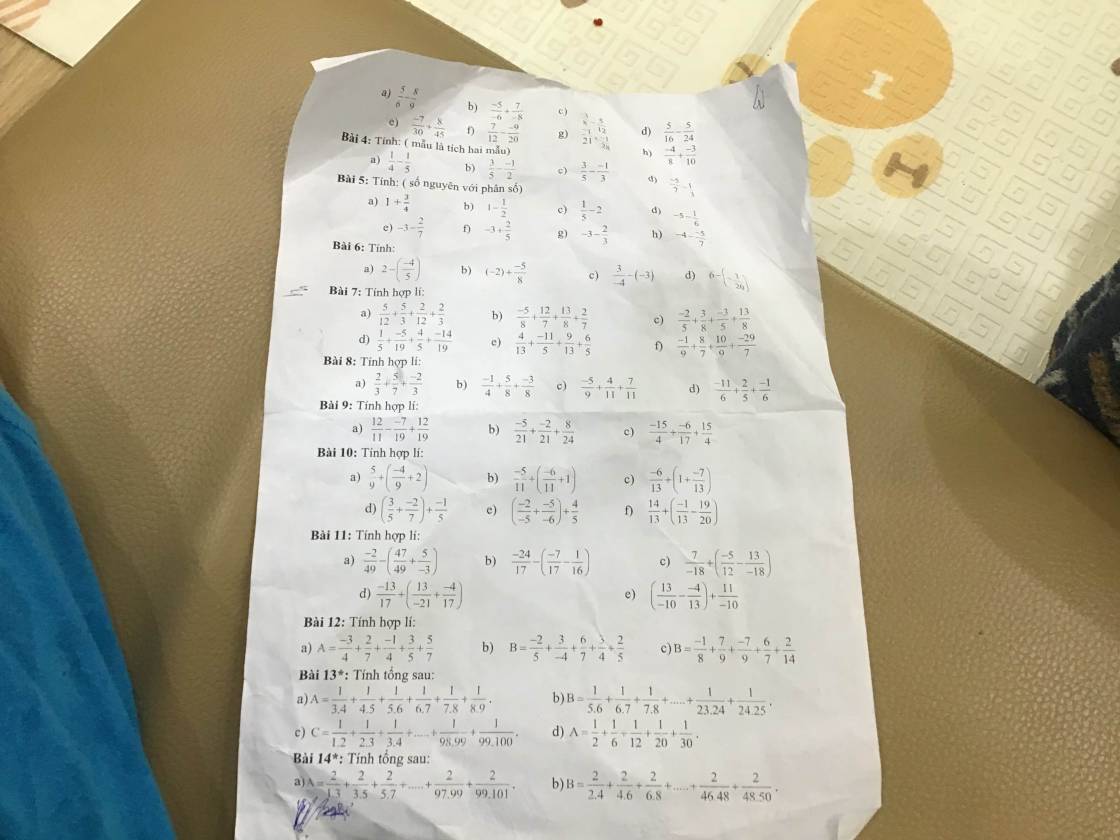
Bài 4:
a; \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) = \(\dfrac{5}{20}\) - \(\dfrac{4}{20}\) = \(\dfrac{1}{20}\)
b; \(\dfrac{3}{5}\) - \(\dfrac{-1}{2}\) = \(\dfrac{6}{10}\) + \(\dfrac{5}{10}\) = \(\dfrac{11}{10}\)
c; \(\dfrac{3}{5}\) - \(\dfrac{-1}{3}\) = \(\dfrac{9}{15}\) + \(\dfrac{5}{15}\) = \(\dfrac{14}{15}\)
d; \(\dfrac{-5}{7}\) - \(\dfrac{1}{3}\)= \(\dfrac{-15}{21}\) - \(\dfrac{7}{21}\)= \(\dfrac{-22}{21}\)
Bài 5
a; 1 + \(\dfrac{3}{4}\) = \(\dfrac{4}{4}\) + \(\dfrac{3}{4}\) = \(\dfrac{7}{4}\) b; 1 - \(\dfrac{1}{2}\) = \(\dfrac{2}{2}\) - \(\dfrac{1}{2}\) = \(\dfrac{1}{2}\)
c; \(\dfrac{1}{5}\) - 2 = \(\dfrac{1}{5}\) - \(\dfrac{10}{5}\) = \(\dfrac{-9}{5}\) d; -5 - \(\dfrac{1}{6}\) = \(\dfrac{-30}{6}\) - \(\dfrac{1}{6}\) = \(\dfrac{-31}{6}\)
e; - 3 - \(\dfrac{2}{7}\)= \(\dfrac{-21}{7}\) - \(\dfrac{2}{7}\)= \(\dfrac{-23}{7}\) f; - 3 + \(\dfrac{2}{5}\) = \(\dfrac{-15}{5}\) + \(\dfrac{2}{5}\)= - \(\dfrac{13}{5}\)
g; - 3 - \(\dfrac{2}{3}\) = \(\dfrac{-9}{3}\) - \(\dfrac{2}{3}\) = \(\dfrac{-11}{3}\) h; - 4 - \(\dfrac{-5}{7}\) = \(\dfrac{-28}{7}\)+ \(\dfrac{5}{7}\) = - \(\dfrac{23}{7}\)

Lời giải:
\(E=\frac{\frac{2013}{1}.\frac{2014}{2}.\frac{2015}{3}....\frac{3012}{1000}}{\frac{1001}{1}.\frac{1002}{2}.\frac{1003}{3}....\frac{3012}{2012}}\\ =\frac{2013.2014.2015....3012}{1001.1002.1003....3012}.\frac{1.2.3...2012}{1.2.3..1000}\\ =\frac{1}{1001.1002...2012}.(1001.1002....2012)=1\)

Chia thành các phần quá sao cho số lượng vở và sách bằng nhau nên số lượng quà là ước chung của \(96,36\).
Mà số lượng quà là nhiều nhất nên là \(ƯCLN\left(96,36\right)\).
Phân tích thành tích các thừa số nguyên tố: \(96=2^5.3,36=2^2.3^2\)
Suy ra \(ƯCLN\left(96,36\right)=2^2.3=12\)
Vậy cô giáo có thể chia nhiều nhất thành \(12\)phần quà, khi đó mỗi phần quà có \(\frac{96}{12}=8\)quyển vở và \(\frac{36}{12}=3\)cuốn sách.

a; \(\dfrac{x-1}{12}\) = \(\dfrac{5}{3}\)
\(x-1\) = \(\dfrac{5}{3}\) \(\times\) 12
\(x\) - 1 = 20
\(x\) = 20 + 1
\(x\) = 21
b; \(\dfrac{-x}{8}\) = \(\dfrac{-50}{x}\)
-\(x\).\(x\) = -50.8
-\(x^2\) = -400
\(x^2\) = 400
\(\left[{}\begin{matrix}x=-20\\x=20\end{matrix}\right.\)
Vậy \(x\) \(\in\) {-20; 20}
c; \(\dfrac{x}{3}\) = \(\dfrac{14}{x+1}\)
\(x\).(\(x\)+1) = 14.3
\(x^2\) + \(x\) = 42
\(x^2\) + \(x\) - 42 = 0
\(x^2\) - 6\(x\) + 7\(x\) - 42 = 0
\(x\).(\(x\) - 6) + 7.(\(x\) - 6) = 0
(\(x\) - 6).(\(x\) + 7) = 0
\(\left[{}\begin{matrix}x-6=0\\x+7=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=6\\x=-7\end{matrix}\right.\)
Vậy \(x\) \(\in\) {-7; 6}
d; \(x-\dfrac{2}{9}\) = \(\dfrac{1}{6}\)
\(x\) = \(\dfrac{1}{6}\) + \(\dfrac{2}{9}\)
\(x\) = \(\dfrac{7}{18}\)
Vậy \(x\) = \(\dfrac{7}{18}\)





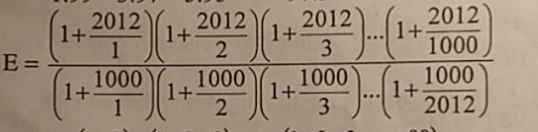
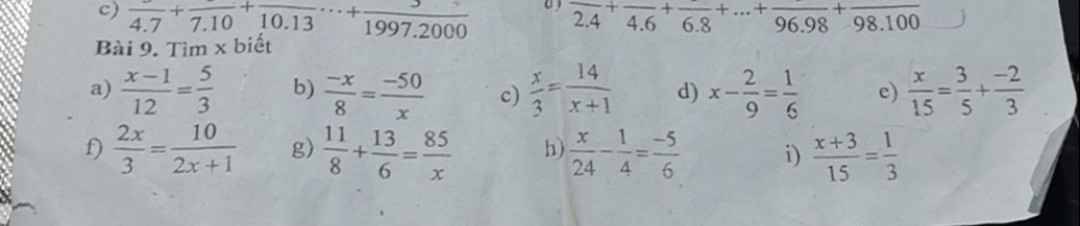
đang phân vân nên chọn áo hay mũ giờ còn thêm nhiều phần quà hấp dẫn quá không biết chọn cái nào ._.
Quạa, cũng muốn đ-được tặng : )