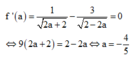Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1/Áp dụng công thức tổng cấp số nhân:
\(z=1+\left(1+i\right)+\left(1+i\right)^2+...+\left(1+i\right)^{20}=1+\frac{\left(1+i\right)^{21}-1}{i+1-1}=1+\frac{\left(1+i\right)^{21}-1}{i}\)
Ta có:
\(\left(1+i\right)^{21}=\left(1+i\right)\left[\left(1+i\right)^2\right]^{10}=\left(1+i\right)\left(1+2i+i^2\right)^{10}\)
\(=\left(1+i\right)\left(2i\right)^{10}=\left(1+i\right).2^{10}.i^{10}=\left(1+i\right)2^{10}\left(i^2\right)^5=-\left(1+i\right).2^{10}\)
\(\Rightarrow z=1+\frac{-\left(1+i\right)2^{10}-1}{i}=1+\frac{-i\left(1+i\right)2^{10}-i}{i^2}=1+\left(i+i^2\right)2^{10}+i=1+i+\left(i-1\right).2^{10}\)
\(\Rightarrow z=\left(1-2^{10}\right)+\left(1+2^{10}\right)i\)
2/
\(z=\left(3+i\sqrt{3}\right)^3\Rightarrow\frac{1}{z}=\frac{1}{\left(3+i\sqrt{3}\right)^3}=\frac{\left(3-i\sqrt{3}\right)^3}{\left(3+i\sqrt{3}\right)^3\left(3-i\sqrt{3}\right)^3}=\frac{\left(3-i\sqrt{3}\right)^3}{\left(9-3i^2\right)^3}\)
\(\Rightarrow\frac{1}{z}=\frac{\left(3-i\sqrt{3}\right)^3}{12^3}=\left(\frac{1}{4}-\frac{\sqrt{3}}{12}i\right)^3\)
3/ Bạn viết lại đề được không?

Lời giải:
Nếu $z_1,z_2,z_3$ là 3 nghiệm phức của pt \(2x^3-3x-2=0\) thì theo định lý Vi-et ta có:
\(\left\{\begin{matrix} z_1+z_2+z_3=0\\ z_1z_2z_3=1\end{matrix}\right.\)
Kết hợp hệ phương trình trên với hằng đẳng thức:
\(z_1^3+z_2^3+z_3^3=(z_1+z_2)^3-3z_1z_2(z_1+z_2)+z_3^3\)
\(=(-z_3)^3-3z_1z_2(-z_3)+z_3^3=3z_1z_2z_3=3\)
Đáp án B



Bài 1:
\(y'=3\left(x+m\right)^2+3\left(x+n\right)^2-3x^2\)
\(y'=3\left(x^2+2mx+m^2\right)+3\left(x^2+2nx+n^2\right)-3x^2\)
\(y'=3\left(x^2+2\left(m+n\right)x+m^2+n^2\right)\)
Để hàm số đồng biến trên R \(\Leftrightarrow y'\ge0\) \(\forall x\in R\)
\(\Rightarrow\Delta'=\left(m+n\right)^2-\left(m^2+n^2\right)\le0\) \(\Rightarrow mn\le0\)
\(P=4\left(m+n\right)^2-\left(m+n\right)-8mn\ge4\left(m+n\right)^2-\left(m+n\right)\ge-\frac{1}{16}\)
Bài 2: Đề bài rất kì quặc
Mình nghĩ cách giải sẽ như sau: nhận thấy \(z=0\) ko phải nghiệm nên chia 2 vế cho \(z^3\):
\(z^3+2016z^2+2017z+2018+\frac{2017}{z}+\frac{2016}{z^2}+\frac{1}{z^3}=0\)
\(\Leftrightarrow z^3+\frac{1}{z^3}+2016\left(z^2+\frac{1}{z^2}\right)+2017\left(z+\frac{1}{z}\right)+2018=0\)
Đặt \(z+\frac{1}{z}=a\Rightarrow\left\{{}\begin{matrix}a^2=z^2+\frac{1}{z^2}+2\Rightarrow z^2+\frac{1}{z^2}=a^2-2\\a^3=z^3+\frac{1}{z^3}+3\left(z+\frac{1}{z}\right)\Rightarrow z^3+\frac{1}{z^3}=a^3-3a\end{matrix}\right.\)
\(\Rightarrow a^3-3a+2016\left(a^2-2\right)+2017a+2018=0\)
\(\Leftrightarrow a^3+2016a^2+2014a-2014=0\)
Đặt \(f\left(a\right)=a^3+2016a^2+2014a-2014\)
\(f\left(-2015\right)=1\) ; \(f\left(-2016\right)=...< 0\)
\(\Rightarrow f\left(-2015\right).f\left(-2016\right)< 0\Rightarrow\) phương trình luôn có ít nhất một nghiệm \(a_0\in\left(-2016;-2015\right)\)
Khi đó ta có: \(z+\frac{1}{z}=a_0\Rightarrow z^2-a_0z+1=0\)
\(\Delta=a_0^2-4>0\) do \(a_0\in\left(-2016;-2015\right)\) nên \(a_0^2>2015^2>4\)
\(\Rightarrow\) Phương trình đã cho có ít nhất 2 nghiệm thực nên ko thể có 6 nghiệm phức
\(\Rightarrow\) Đề bài sai :(

Theo Viet: \(\left\{{}\begin{matrix}z_1+z_2=2i\\z_1z_2=-1-2i\end{matrix}\right.\)
\(\Rightarrow z_1^3+z_2^3=\left(z_1+z_2\right)\left(z_1^2+z_2^2-z_1z_2\right)=\left(z_1+z_2\right)\left(\left(z_1+z_2\right)^2-3z_1z_1\right)\)
\(=2i\left[\left(2i\right)^2-3\left(-1-2i\right)\right]=2i\left(6i-1\right)=-12-2i\)