Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
a: \(\Leftrightarrow\left\{{}\begin{matrix}2-x+y-3x-3y=5\\3x-3y+5x+5y=-2\end{matrix}\right.\)
=>-4x-2y=3 và 8x+2y=-2
=>x=1/4; y=-2
b: \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{y-1}=1\\\dfrac{1}{x-2}+\dfrac{1}{y-1}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y-1=5\\\dfrac{1}{x-2}=1-\dfrac{1}{5}=\dfrac{4}{5}\end{matrix}\right.\)
=>y=6 và x-2=5/4
=>x=13/4; y=6
c: =>x+y=24 và 3x+y=78
=>-2x=-54 và x+y=24
=>x=27; y=-3
d: \(\Leftrightarrow\left\{{}\begin{matrix}2\sqrt{x-1}-6\sqrt{y+2}=4\\2\sqrt{x-1}+5\sqrt{y+2}=15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-11\sqrt{y+2}=-11\\\sqrt{x-1}=2+3\cdot1=5\end{matrix}\right.\)
=>y+2=1 và x-1=25
=>x=26; y=-1

a)\(\left\{{}\begin{matrix}\dfrac{10}{\sqrt{12x-3}}+\dfrac{5}{\sqrt{4y+1}}=1\\\dfrac{7}{\sqrt{12x-3}}+\dfrac{8}{\sqrt{4y+1}}=1\end{matrix}\right.\)
ĐK: \(x>\dfrac{1}{4};y>-\dfrac{1}{4}\), đặt \(a=\dfrac{1}{\sqrt{12x-3}};b=\dfrac{1}{\sqrt{4y+1}}\)với a,b>0
khi đó, ta có hệ phương mới \(\left\{{}\begin{matrix}10a+5b=1\\7a+8b=1\end{matrix}\right.\)
\(\left\{{}\begin{matrix}10a+5b=1\\7a+8b=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}80a+40b=8\\35a+40b=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}45a=3\\35a+40b=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{15}\\35a+40b=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{15}\\35.\dfrac{1}{15}+40b=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{15}\\b=\dfrac{1}{15}\end{matrix}\right.\)
thay \(\dfrac{1}{\sqrt{12x-3}}=a\) hay \(\dfrac{1}{\sqrt{12x-3}}=\dfrac{1}{15}\Rightarrow\sqrt{12x-3}=15\Leftrightarrow12x-3=225\Leftrightarrow12x=228\Leftrightarrow x=19\left(TMĐK\right)\) thay \(\dfrac{1}{\sqrt{4y+1}}=b\) hay
\(\dfrac{1}{\sqrt{4y+1}}=\dfrac{1}{15}\Rightarrow\sqrt{4y+1}=15\Leftrightarrow4y+1=225\Leftrightarrow4y=224\Leftrightarrow y=56\left(TMĐK\right)\)
Vậy (x;y)=(9;56) là nghiệm duy nhất của hệ phương trình đã cho.
b)\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=4\\x\left(1+4y\right)+y=2\end{matrix}\right.\)
ĐK: x,y#0, khi đó \(\dfrac{1}{x}+\dfrac{1}{y}=4\Rightarrow x+y=4xy\)
Do đó \(x\left(1+4y\right)+y=2\Leftrightarrow x+4xy+y=2\Leftrightarrow x+x+y+y=2\Leftrightarrow2\left(x+y\right)=2\Leftrightarrow x+y=1\)
Mà \(4xy=x+y\Leftrightarrow4xy=1\Leftrightarrow xy=\dfrac{1}{4}\)
Vậy \(x+y=1;xy=\dfrac{1}{4}\)
Do đó x,y là nghiệm của phương trình:
\(t^2-t+\dfrac{1}{4}=0\)
\(\Delta=b^2-4ac=1-4.1.\dfrac{1}{4}=0\)
Phương trình có nghiêm kép \(x_1=x_2=-\dfrac{b}{2a}=-\dfrac{-1}{2}=\dfrac{1}{2}\)
\(\Rightarrow x=y=\dfrac{1}{2}\left(nhận\right)\)
Vậy (x;y)=\(\left(\dfrac{1}{2};\dfrac{1}{2}\right)\) là nghiệm duy nhất của hệ phương trình đã cho.

a. Pt đã cho tương đương với:
\(\sqrt{3x-2}=\sqrt{x+7}+1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{2}{3}\\3x-2=x+7+1+2\sqrt{x+7}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{2}{3}\\2x-10=2\sqrt{x+7}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{2}{3}\\x-5=\sqrt{x+7}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge5\\x^2-10x+25=x+7\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge5\\x^2-11x+18=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge5\\\left(x-2\right)\left(x-9\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge5\\\left[{}\begin{matrix}x=2\\x=9\end{matrix}\right.\end{matrix}\right.\)(Loại )
\(\Leftrightarrow x=9\)
Vậy pt có nghiệm x =9
b. Đk: \(x\ne1;y\ne2\)
Đặt \(\dfrac{1}{x-1}=a;\dfrac{1}{y-2}=b\)
Khi đó hệ đã cho trở thành:
\(\left\{{}\begin{matrix}a+b=2\\-3a+2b=1\end{matrix}\right.\)
Giải hệ trên tìm a,b rồi từ đó tìm được x;y. Nhớ đối chiếu với Đk trước khi kết luận.

\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x-1}-\dfrac{13}{y-2}=\dfrac{2}{5}-1=-\dfrac{3}{5}\\\dfrac{-8}{x-1}+\dfrac{30}{y-2}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-1=\dfrac{-16}{5}\\y-2=-20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{11}{5}\\y=-18\end{matrix}\right.\)

hỏi trước tí, bạn biết giải cái hệ này chứ?
\(\left\{{}\begin{matrix}2x+y=3\\2x-3y=1\end{matrix}\right.\)
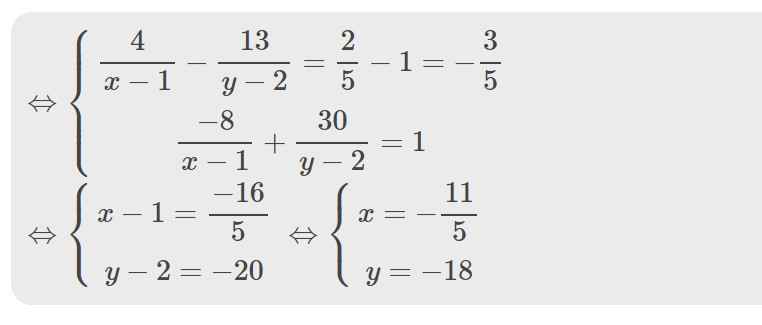
\(x+y=11=>y=11-x\left(1\right)\)
có: \(\dfrac{x}{10}+\dfrac{y}{15}=1\left(2\right)\)
thế(1) vào(2)=>\(\dfrac{x}{10}+\dfrac{11-x}{15}=1< =>\dfrac{3x+22-2x}{30}=1\)
\(=>x+22=30=>x=8\)(3)
thế (3) vào(1)=>y\(=11-8=3\)
\(\left\{{}\begin{matrix}x+y=11\\\dfrac{1}{10}x+\dfrac{1}{15}y=1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{10}x+\dfrac{1}{10}y=\dfrac{11}{10}\left(1\right)\\\dfrac{1}{10}x+\dfrac{1}{15}y=1\left(2\right)\end{matrix}\right.\)
Lấy \(\left(1\right)-\left(2\right)\Rightarrow\dfrac{1}{30}x=\dfrac{1}{10}\Rightarrow x=3\Rightarrow y=11-3=8\)