K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
27 tháng 9 2023
Thực hiện các bước đã nêu ở phương pháp ta có các hình dưới đây
a) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía trên, cắt trục tung và trục hoành lần lượt tại điểm có tọa độ là (0; 2) và (2; 0)
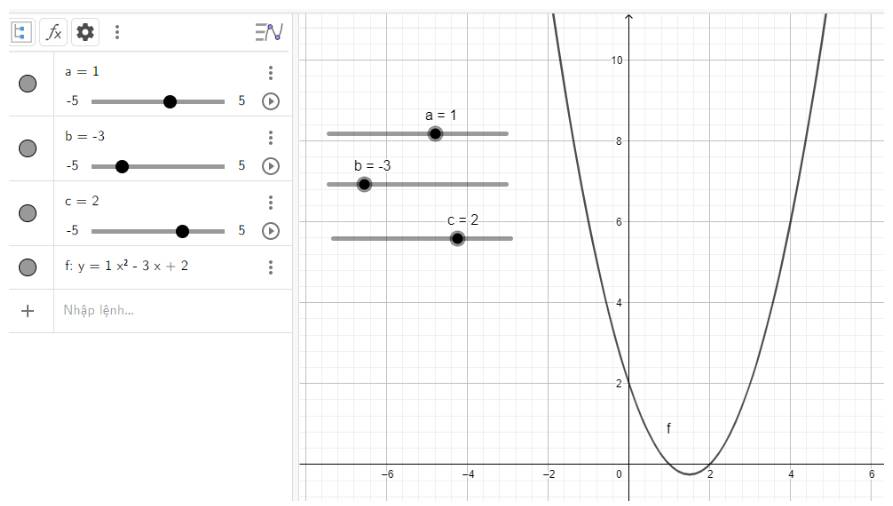
b) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía trên, đi qua gốc tọa độ và đỉnh chính là gốc tọa độ
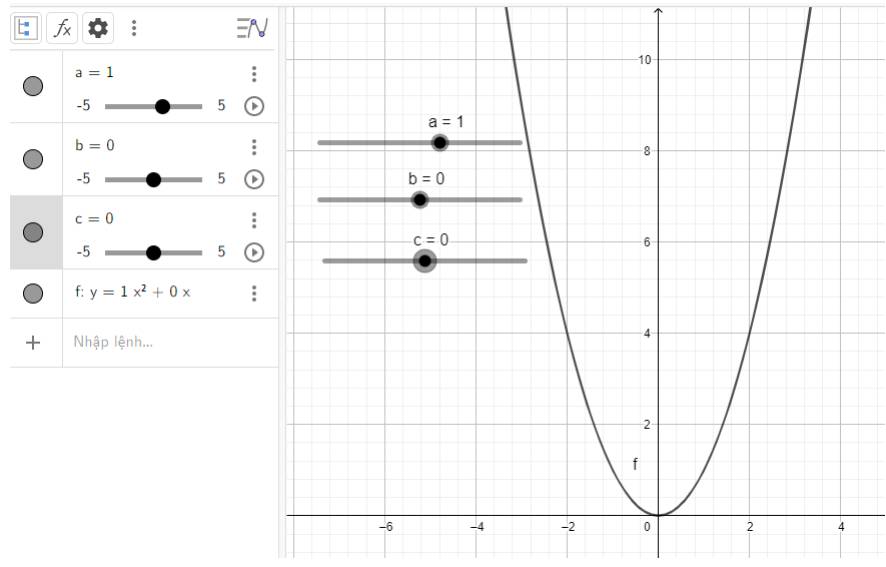
c) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía dưới, đi qua gốc tọa độ và đỉnh chính là gốc tọa độ
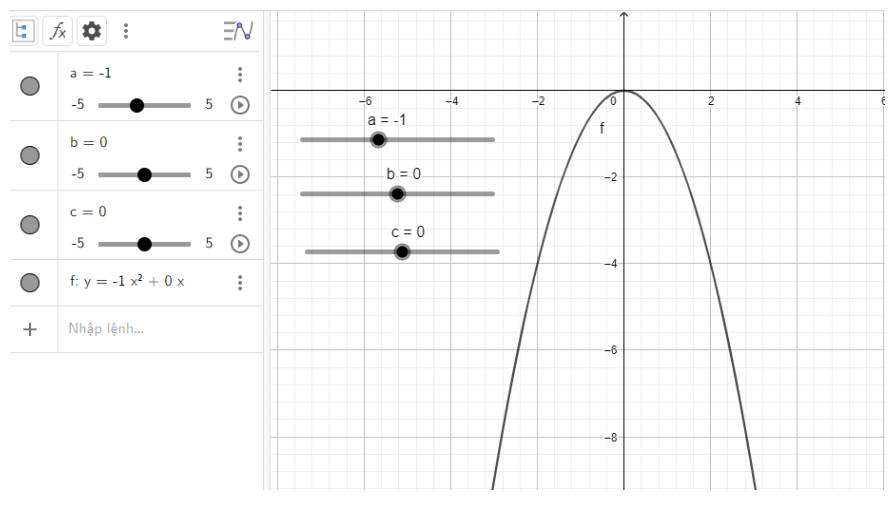
d) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía trên, cắt trục tung tại điểm có tung độ là 1 đó cũng chính là đỉnh của parabol
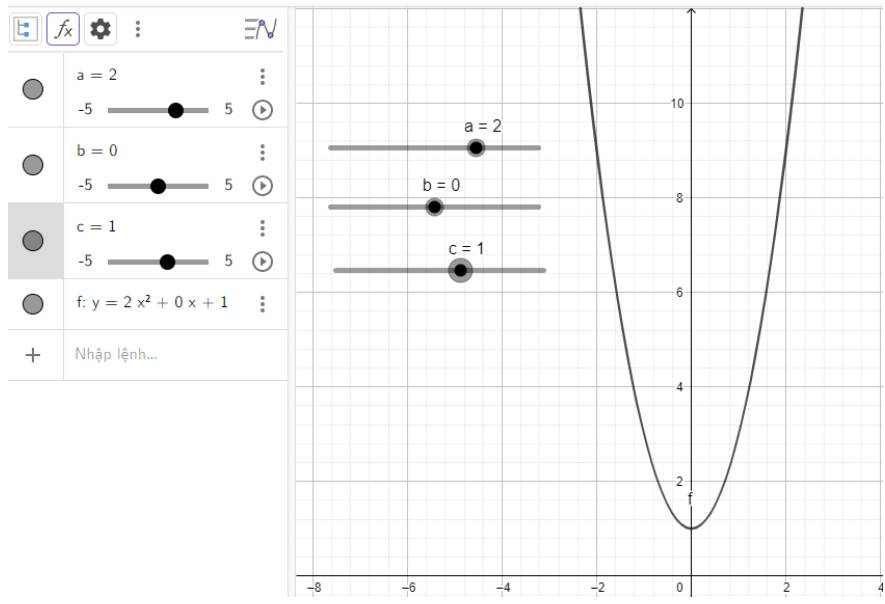
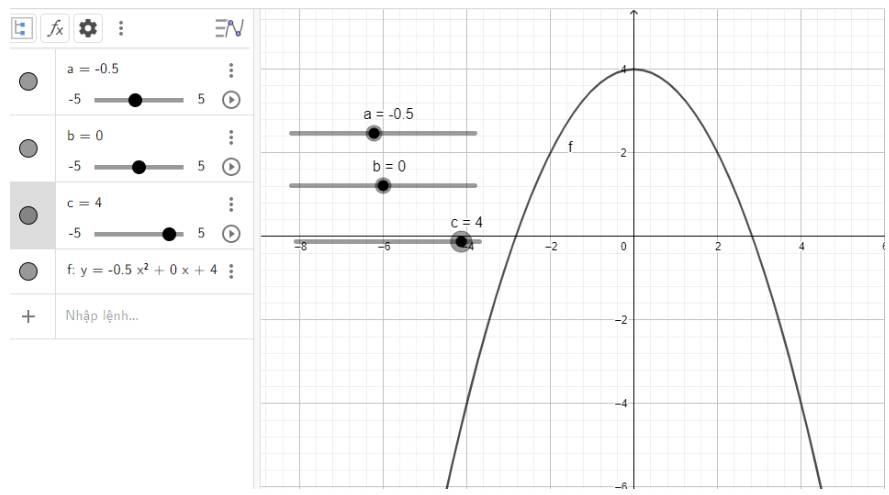
e) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía dưới, cắt trục tung tại điểm có tung độ là 4 đó cũng chính là đỉnh của parabol
9 tháng 11 2018
1) \(\left\{{}\begin{matrix}x+y=1\\x^3+y^3=x^2+y^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=1\\\left(x+y\right)\left(x^2-xy+y^2\right)-\left(x^2+y^2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=1\\x^2-xy+y^2-x^2-y^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=1\\xy=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=1\\\left[{}\begin{matrix}x=0\\y=0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+y=1\\x=0\end{matrix}\right.\\\left\{{}\begin{matrix}x+y=1\\y=0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\\\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\end{matrix}\right.\)
2) \(\left\{{}\begin{matrix}x^2+y^2=5\\x^4-x^2y^2+y^4=13\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+y^2=5\\\left(x^2+y^2\right)^2-3x^2y^2=13\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+y^2=5\\\left(5\right)^2-3x^2y^2=13\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+y^2=5\\-3x^2y^2=-12\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2=5-y^2\\x^2y^2=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2=5-y^2\\\left(5-y^2\right)y^2=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2=5-y^2\\-y^4+5y^2-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2=5-y^2\\-y^4+5y^2-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2=5-y^2\\\left[{}\begin{matrix}y^2=1\\y^2=4\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x^2=5-y^2\\y^2=1\end{matrix}\right.\\\left\{{}\begin{matrix}x^2=5-y^2\\y^2=4\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x^2=4\\y^2=1\end{matrix}\right.\\\left\{{}\begin{matrix}x^2=1\\y^2=4\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\\\left[{}\begin{matrix}y=1\\y=-1\end{matrix}\right.\end{matrix}\right.\\\left\{{}\begin{matrix}\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\\\left[{}\begin{matrix}y=2\\y=-2\end{matrix}\right.\end{matrix}\right.\end{matrix}\right.\)
vậy \(S=\left\{\left(2;1\right),\left(2;-1\right),\left(-2;1\right),\left(-2;-1\right),\left(1;2\right),\left(1;-2\right),\left(-1;2\right),\left(-1;-2\right)\right\}\)
9 tháng 11 2018
4) \(\left\{{}\begin{matrix}x^5+y^5=1\\x^9+y^9=x^4+y^4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^5-1=-y^5\\x^9-x^4+y^9-y^4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left\{{}\begin{matrix}x^5-1=-y^5\\y^5-1=-x^5\end{matrix}\right.\\x^4\left(x^5-1\right)+y^4\left(y^5-1\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^5+y^5=1\\x^4\left(-y^5\right)+y^4\left(-x^5\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^5+y^5=1\\-x^4y^4\left(x+y\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^5+y^5=1\\\left[{}\begin{matrix}x=0\\y=0\\x+y=0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x^5+y^5=1\\x=0\end{matrix}\right.\\\left\{{}\begin{matrix}x^5+y^5=1\\y=0\end{matrix}\right.\\\left\{{}\begin{matrix}x^5+y^5=1\\x=-y\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\\\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\\\left\{{}\begin{matrix}x=-y\\x^5-x^5=1\end{matrix}\right.\end{matrix}\right.\)
vậy \(S=\left\{\left(1;0\right),\left(0;1\right)\right\}\)
19 tháng 7
ta có:x+y+z=0⇒x+y=-z⇔(x+y)2=z2⇔x2+2xy+y2-z2=0
⇒x2+y2-z2=-2xy(1)
CMTT:⇒y2+z2-x2=-2yz(2) và z2+x2-y2=-2xz(3)
Thay (1)(2)(3) vào B,ta có.B=-(2xy.2yz.2xz)/16xyz=-xyz/2