Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

*Xét hàm số: y= -x3 + 2x2 – x – 7
Tập xác định: D = R
\(y'\left(x\right)=-3x^2+4x-1\); \(y'\left(x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{3}\end{matrix}\right.\)
y’ > 0 với và y’ < 0 với \(x \in ( - \infty ,{1 \over 3}) \cup (1, + \infty )
Vậy hàm số đồng biến trong (\(\dfrac{1}{3}\),1)(\(\dfrac{1}{3}\),1) và nghịch biến trong (−∞,13)∪(1,+∞)(−∞,13)b) Xét hàm số: \(y=\dfrac{x-5}{1-x}\).
Tập xác định: D = R{1}
\(y'=\dfrac{-4}{\left(1-x\right)^2}< 0,\forall x\in D\)
Vậy hàm số nghịch biến trong từng khoảng (-∞,1) và (1, +∞)

1. a) Tập xác định : D = R; y' = 3 - 2x => y' = 0 ⇔ x = \(\dfrac{3}{2}\).
Bảng biến thiên :
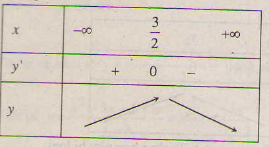
Hàm số đồng biến trên khoảng (-∞; \(\dfrac{3}{2}\)); nghịch biến trên khoảng ( \(\dfrac{3}{2}\); +∞ ).
b) Tập xác định D = R;
y'= x2 + 6x - 7 => y' = 0 ⇔ x = 1, x = -7.
Bảng biến thiên :
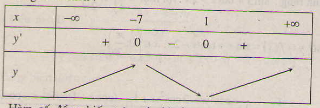
Hàm số đồng biến trên các khoảng (-∞ ; -7), (1 ; +∞) ; nghịch biến trên các khoảng (-7 ; 1).
c) Tập xác định : D = R.
y' = 4x3 - 4x = 4x(x2 - 1) => y' = 0 ⇔ x = -1, x = 0, x = 1.
Bảng biến thiên: tự vẽ.
Hàm số đồng biến trên các khoảng (-1 ; 0), (1 ; +∞) ; nghịch biến trên các khoảng (-∞ ; -1), (0 ; 1).
d) Tập xác định : D = R. y' = -3x2 + 2x => y' = 0 ⇔ x = 0, x = \(\dfrac{2}{3}\).
Bảng biến thiên :
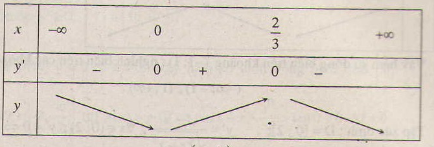
Hàm số đồng biến trên khoảng ( 0 ; \(\dfrac{2}{3}\) ) ; nghịch biến trên các khoảng (-∞ ; 0), ( \(\dfrac{2}{3}\); +∞).
1. a) Tập xác định : D = R; y' = 3 - 2x => y' = 0 ⇔ x = \(\dfrac{3}{2}\).
Bảng biến thiên :

Hàm số đồng biến trên khoảng (-∞; \(\dfrac{3}{2}\)); nghịch biến trên khoảng ( \(\dfrac{3}{2}\); +∞ ).
b) Tập xác định D = R;
y'= x2 + 6x - 7 => y' = 0 ⇔ x = 1, x = -7.
Bảng biến thiên :

Hàm số đồng biến trên các khoảng (-∞ ; -7), (1 ; +∞) ; nghịch biến trên các khoảng (-7 ; 1).
c) Tập xác định : D = R.
y' = 4x3 - 4x = 4x(x2 - 1) => y' = 0 ⇔ x = -1, x = 0, x = 1.
Bảng biến thiên: tự vẽ.
Hàm số đồng biến trên các khoảng (-1 ; 0), (1 ; +∞) ; nghịch biến trên các khoảng (-∞ ; -1), (0 ; 1).
d) Tập xác định : D = R. y' = -3x2 + 2x => y' = 0 ⇔ x = 0, x = 2323.
Bảng biến thiên :

Hàm số đồng biến trên khoảng ( 0 ; \(\dfrac{2}{3}\) ) ; nghịch biến trên các khoảng (-∞ ; 0), ( \(\dfrac{2}{3}\); +∞).

a) Tập xác định: D = R\{m}
Hàm số đồng biến trên từng khoảng (−∞;m),(m;+∞)(−∞;m),(m;+∞)khi và chỉ khi:
y′=−m2+4(x−m)2>0⇔−m2+4>0⇔m2<4⇔−2<m<2y′=−m2+4(x−m)2>0⇔−m2+4>0⇔m2<4⇔−2<m<2
b) Tập xác định: D = R\{m}
Hàm số nghịch biến trên từng khoảng khi và chỉ khi:
y′=−m2+5m−4(x+m)2<0⇔−m2+5m−4<0y′=−m2+5m−4(x+m)2<0⇔−m2+5m−4<0
[m<1m>4[m<1m>4
c) Tập xác định: D = R
Hàm số nghịch biến trên R khi và chỉ khi:
y′=−3x2+2mx−3≤0⇔′=m2−9≤0⇔m2≤9⇔−3≤m≤3y′=−3x2+2mx−3≤0⇔′=m2−9≤0⇔m2≤9⇔−3≤m≤3
d) Tập xác định: D = R
Hàm số đồng biến trên R khi và chỉ khi:
y′=3x2−4mx+12≥0⇔′=4m2−36≤0⇔m2≤9⇔−3≤m≤3

ta tính \(y'=3x^2-4x+1\)
\(y'=0\Rightarrow3x^2-4x+1=0\Rightarrow x=1;x=\frac{1}{3}\)
ta có
ta có trong khoảng 2 nghiệm thì y' cùng dấu với hệ số a, ngoài khoảng 2 nghiệm trái dấu với hệ số a
suy ra f'(x)>0 với \(x\in\left(-\infty;\frac{1}{3}\right)\cup\left(1;+\infty\right)\) suy ra hàm số đồng biến trên \(\left(-\infty;\frac{1}{3}\right)\cup\left(1;+\infty\right)\)
lại có f'(x)<0 với \(x\in\left(\frac{1}{3};1\right)\) suy ra hàm số nghịch biến trên \(\left(\frac{1}{3};1\right)\)







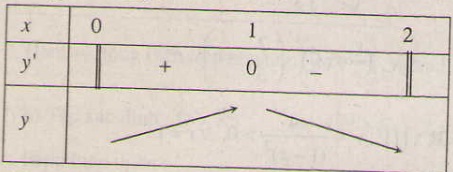
TXĐ: R
y′ = 6x − 24 x 2 = 6x(1 − 4x)
y' = 0 ⇔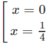
y' > 0 trên khoảng (0; 1/4) , suy ra y đồng biến trên khoảng (0; 1/4)
y' < 0 trên các khoảng (- ∞ ; 0 ); (14; + ∞ ), suy ra y nghịch biến trên các khoảng (- ∞ ;0 ); (14;+ ∞ )