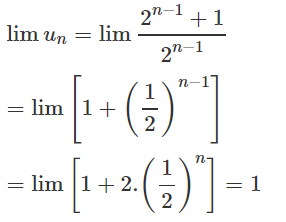Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số xấu thế nhỉ?
\(u_n=v_n+\dfrac{\sqrt{5}-3}{2}\)
\(\Rightarrow v_{n+1}+\dfrac{\sqrt{5}-3}{2}=-\dfrac{1}{3+v_n+\dfrac{\sqrt{5}-3}{2}}\)
\(\Rightarrow\left\{{}\begin{matrix}v_1=u_1-\dfrac{\sqrt{5}-3}{2}=\dfrac{5-\sqrt{5}}{2}\\v_{n+1}=\dfrac{\dfrac{3-\sqrt{5}}{2}v_n}{\dfrac{3+\sqrt{5}}{2}+v_n}\end{matrix}\right.\)
\(v_n=\dfrac{1}{y_n}\Rightarrow\dfrac{1}{y_{n+1}}=\dfrac{\dfrac{3-\sqrt{5}}{2}.\dfrac{1}{y_n}}{\dfrac{3+\sqrt{5}}{2}+\dfrac{1}{y_n}}\)
\(\Rightarrow\dfrac{1}{y_{n+1}}=\dfrac{3-\sqrt{5}}{2y_n\left(\dfrac{3+\sqrt{5}}{2}+\dfrac{1}{y_n}\right)}=\dfrac{3-\sqrt{5}}{\left(3+\sqrt{5}\right)y_n+2}\)
\(\Leftrightarrow y_{n+1}=\dfrac{\left(3+\sqrt{5}\right)y_n}{3-\sqrt{5}}+\dfrac{2}{3-\sqrt{5}}\)
\(\Rightarrow\left\{{}\begin{matrix}y_1=\dfrac{1}{v_1}=\dfrac{2}{5-\sqrt{5}}\\y_{n+1}=\dfrac{3+\sqrt{5}}{3-\sqrt{5}}y_n+\dfrac{2}{3-\sqrt{5}}\end{matrix}\right.\)
\(z_n=y_n+\dfrac{\sqrt{5}}{5}\Rightarrow\left\{{}\begin{matrix}z_1=y_1+\dfrac{\sqrt{5}}{5}=\dfrac{5+3\sqrt{5}}{10}\\z_{n+1}=\dfrac{3+\sqrt{5}}{3-\sqrt{5}}z_n\end{matrix}\right.\)
\(\Rightarrow z_n:csn-co:\left\{{}\begin{matrix}z_1=\dfrac{5+3\sqrt{5}}{10}\\q=\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\end{matrix}\right.\)
\(\Rightarrow z_{n+1}=\dfrac{5+3\sqrt{5}}{10}.\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)^n\)
\(\Rightarrow y_{n+1}=z_{n+1}-\dfrac{\sqrt{5}}{5}=\dfrac{5+3\sqrt{5}}{10}\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)^n-\dfrac{\sqrt{5}}{5}\)
\(v_{n+1}=\dfrac{1}{y_{n+1}}=\dfrac{1}{\dfrac{5+3\sqrt{5}}{10}\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)^n-\dfrac{\sqrt{5}}{5}}\)
\(u_{n+1}=v_{n+1}+\dfrac{\sqrt{5}-3}{2}=\dfrac{1}{\dfrac{5+3\sqrt{5}}{10}\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)^n-\dfrac{\sqrt{5}}{5}}+\dfrac{\sqrt{5}-3}{2}\)
Xét:
\(u_{n+2}-u_{n+1}=\dfrac{1}{\dfrac{5+3\sqrt{5}}{10}.\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)^n.\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)-\dfrac{\sqrt{5}}{5}}+\dfrac{\sqrt{5}-2}{2}-\dfrac{1}{\dfrac{5+3\sqrt{5}}{10}\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)^n-\dfrac{\sqrt{5}}{5}}-\dfrac{\sqrt{5}-2}{2}\)
\(=\dfrac{1}{\dfrac{5+3\sqrt{5}}{10}\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)^n.\dfrac{3+\sqrt{5}}{3-\sqrt{5}}-\dfrac{\sqrt{5}}{5}}-\dfrac{1}{\dfrac{5+3\sqrt{5}}{10}\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)^n-\dfrac{\sqrt{5}}{5}}\)
\(=\dfrac{\dfrac{5+3\sqrt{5}}{10}\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)^n-\dfrac{5+3\sqrt{5}}{10}\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)^n.\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)}{.....}\)
\(=\dfrac{\dfrac{5+3\sqrt{5}}{10}\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)^n\left(1-\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)}{....}=\dfrac{\dfrac{5+3\sqrt{5}}{10}\left(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}\right)^n.\left(-\dfrac{5+3\sqrt{5}}{2}\right)}{...}< 0\)
\(\Rightarrow\) dãy giảm
\(\Rightarrow u_1>u_2>....>u_n\)
\(\Rightarrow\lim\limits u_n=1\)
Bn tham khảo đây nhé: https://diendantoanhoc.org/topic/140204-t%C3%A0i-li%E1%BB%87u-d%C3%A3y-s%E1%BB%91/

\(u_n-u_{n+1}=u_n+\left(1-u_{n+1}\right)-1\ge2\sqrt{u_n\left(1-u_{n+1}\right)}-1>0\)
\(\Rightarrow u_n>u_{n+1}\Rightarrow\) dãy giảm
Dãy giảm và bị chặn dưới bởi 0 nên có giới hạn hữu hạn.
Gọi giới hạn đó là k
\(\Rightarrow k\left(1-k\right)\ge\dfrac{1}{4}\Rightarrow\left(2k-1\right)^2\le0\Rightarrow k=\dfrac{1}{2}\)
Vậy \(\lim\left(u_n\right)=\dfrac{1}{2}\)

Ta sẽ chứng minh dãy bị chặn trên bởi 2
Thật vậy, với \(n=1;2\) thỏa mãn
Giả sử điều đó cũng đúng với \(n=k\) , tức \(u_k< 2\)
Ta cần chứng minh \(u_{k+1}< 2\)
Ta có: \(u_{k+1}=\sqrt{3u_k-2}< \sqrt{3.2-2}=2\) (đpcm)
Tương tự, ta cũng quy nạp được dễ dàng \(u_n>1\)
Mặt khác: \(u_n-u_{n-1}=\sqrt{3u_{n-1}-2}-u_{n-1}=\dfrac{3u_{n-1}-2-u_{n-1}^2}{\sqrt{3u_{n-1}-2}+u_{n-1}}\)
\(=\dfrac{\left(2-u_{n-1}\right)\left(u_{n-1}-1\right)}{\sqrt{3u_{n-1}-2}+u_{n-1}}>0\)
\(\Rightarrow u_n>u_{n-1}\Rightarrow\) dãy tăng
Dãy tăng và bị chặn trên nên có giới hạn hữu hạn.
Gọi giới hạn đó là k thì:
\(k=\sqrt{3k-2}\Leftrightarrow k=2\)

1) Có \(u_{n+1}-u_n=\dfrac{1}{2}u^2_n-2u_n+2=\dfrac{1}{2}\left(u_n-2\right)^2\) (1)
+) CM \(u_n>2\) (n thuộc N*)
n=1 : u1= 5/2 > 2 (đúng)
Giả sử n=k, uk > 2 (k thuộc N*)
Ta cần CM n = k + 1. Thật vậy ta có:
\(u_{k+1}=\dfrac{1}{2}u^2_k-u_k+2=\dfrac{1}{2}\left(u_k-2\right)^2+u_k\) (đúng)
Vậy un > 2 (n thuộc N*) (2)
Từ (1) (2) => un+1 - un > 0, hay un+1 > un
=> (un) là dãy tăng => \(\lim\limits_{n\rightarrow\infty}u_n=+\infty\)
2) \(2u_{n+1}=u^2_n-2u_n+4\)
\(\Leftrightarrow2u_{n+1}-4=u^2_n-2u_n\)
\(\Leftrightarrow2\left(u_{n+1}-2\right)=u_n\left(u_n-2\right)\)
\(\Leftrightarrow\dfrac{1}{u_{n+1}-2}=\dfrac{2}{u_n\left(u_n-2\right)}=\dfrac{1}{u_n-2}-\dfrac{1}{u_n}\)
\(\Leftrightarrow\dfrac{1}{u_n}=\dfrac{1}{u_n-2}-\dfrac{1}{u_{n+1}-2}\)
\(S=\dfrac{1}{u_1}+\dfrac{1}{u_2}+...+\dfrac{1}{u_n}\)
\(=\dfrac{1}{u_1-2}-\dfrac{1}{u_2-2}+\dfrac{1}{u_2-2}+...-\dfrac{1}{u_{n+1}-2}\)
\(=\dfrac{1}{u_1-2}-\dfrac{1}{u_{n+1}-2}\)
\(=2-\dfrac{1}{u_{n+1}-2}\)
\(\Leftrightarrow\lim\limits_{n\rightarrow\infty}S=2\)

\(u_{n+1}=\dfrac{u_n}{u_n+1}\Rightarrow\dfrac{1}{u_{n+1}}=\dfrac{1}{u_n}+1\)
Đặt \(\dfrac{1}{u_n}=v_n\Rightarrow\left\{{}\begin{matrix}v_1=\dfrac{1}{u_1}=1\\v_{n+1}=v_n+1\end{matrix}\right.\)
\(\Rightarrow v_n\) là CSC với công sai \(d=1\Rightarrow v_n=v_1+\left(n-1\right).1=n\)
\(\Rightarrow u_n=\dfrac{1}{n}\)
\(\Rightarrow u_n+1=\dfrac{n+1}{n}\)
\(\lim\dfrac{2014\left(\dfrac{2}{1}\right)\left(\dfrac{3}{2}\right)\left(\dfrac{4}{3}\right)...\left(\dfrac{n+1}{n}\right)}{2015n}=\lim\dfrac{2014\left(n+1\right)}{2015n}=\dfrac{2014}{2015}\)
https://hoc24.vn/cau-hoi/giai-phuong-trinhleft3-4sin2xrightleft3-4sin23xright1-2cos10x.4916575957961
Giúp mik bài này với ạ