
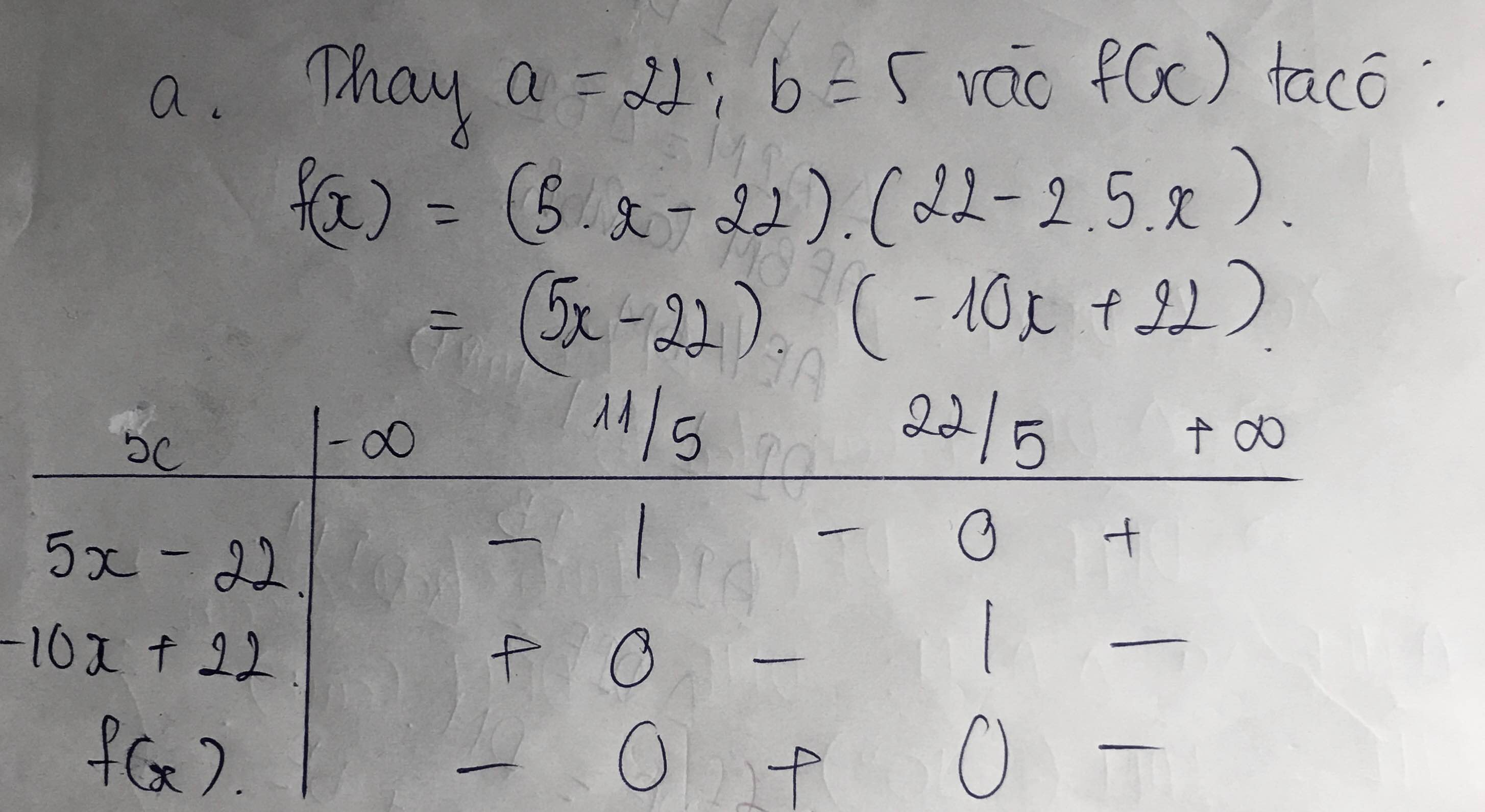
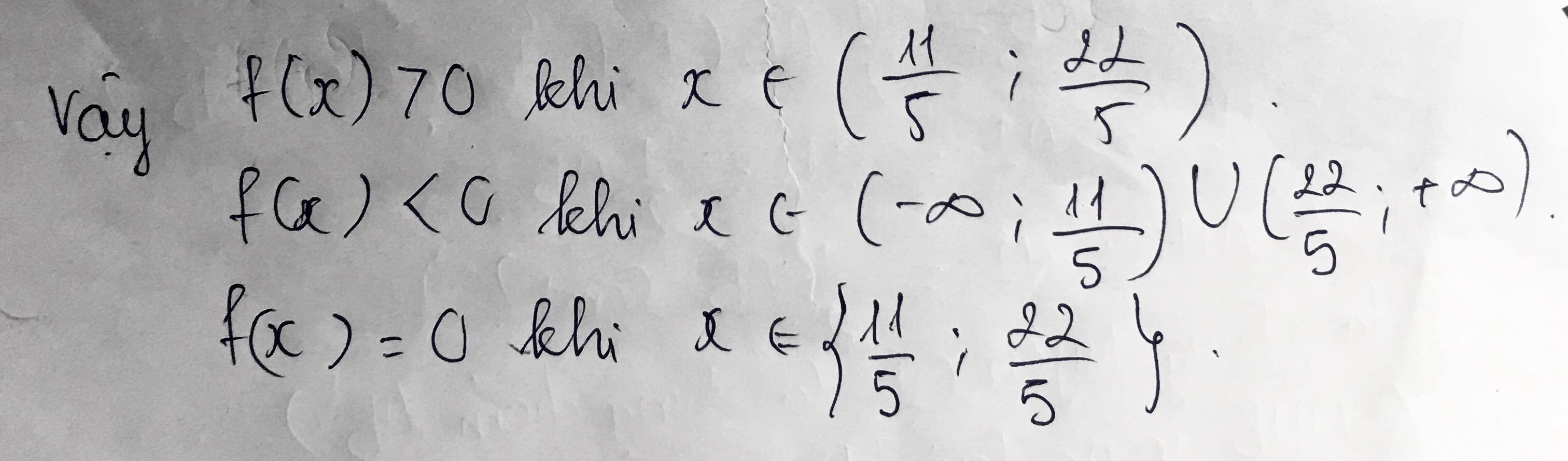
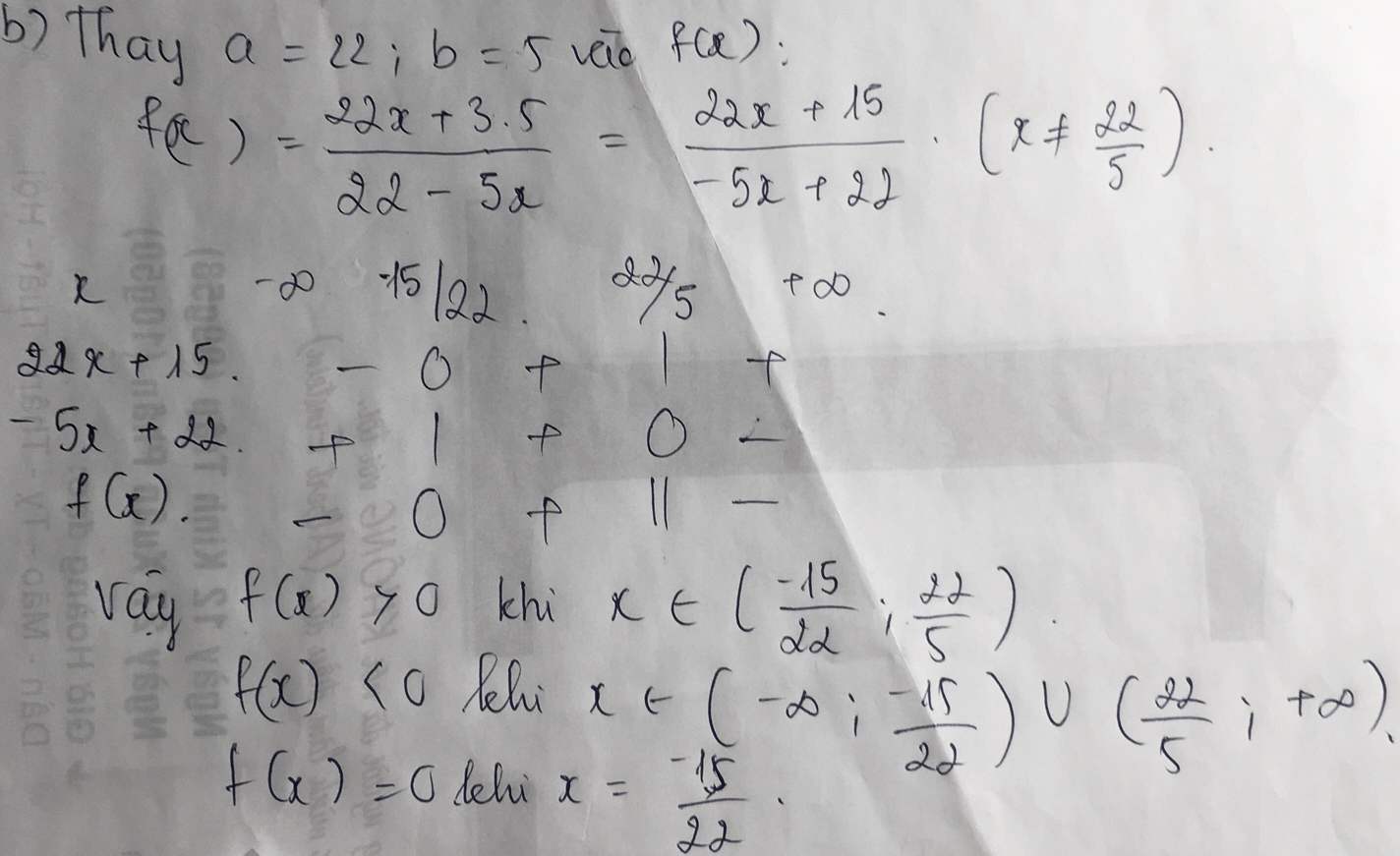
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

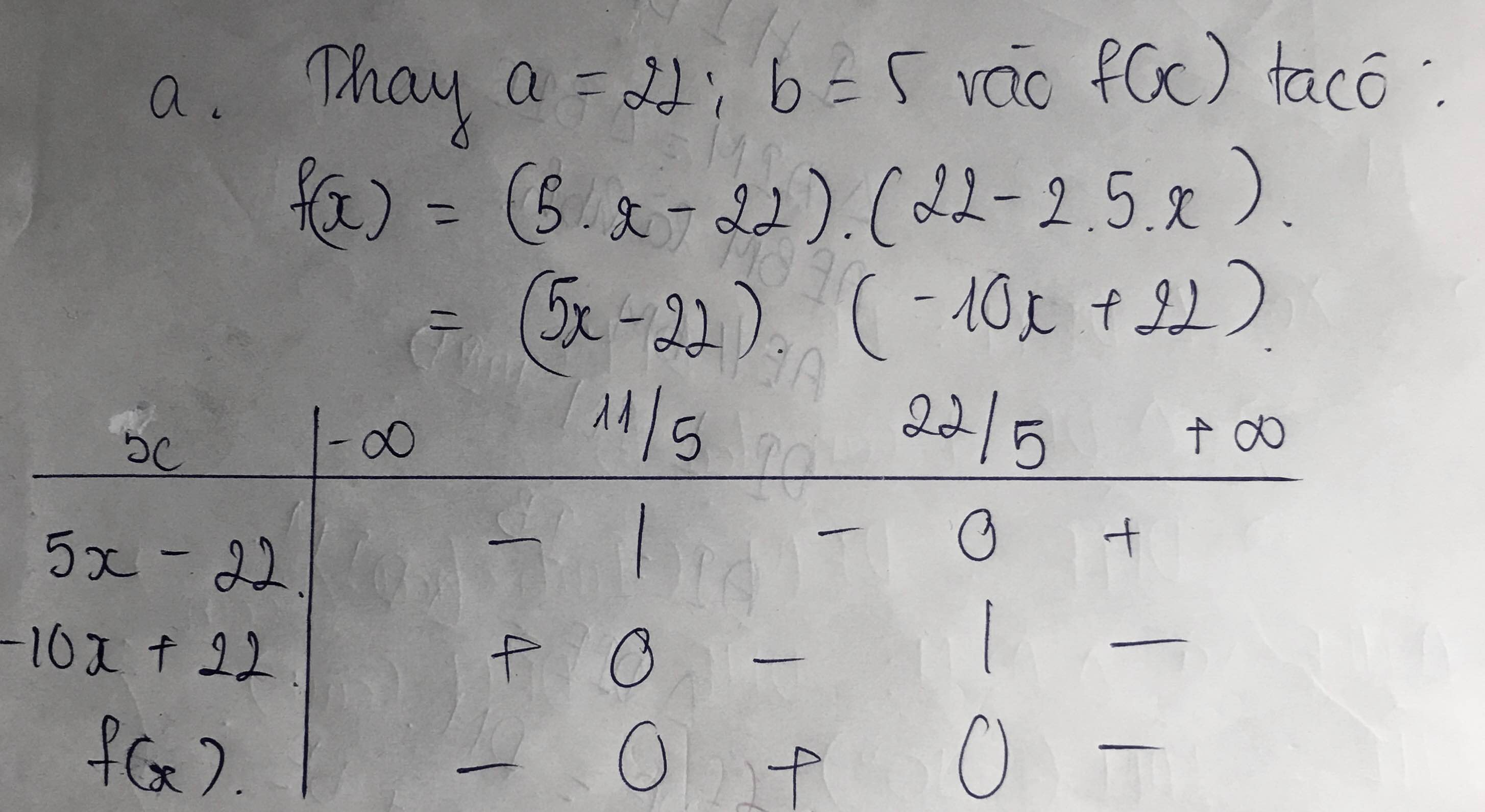
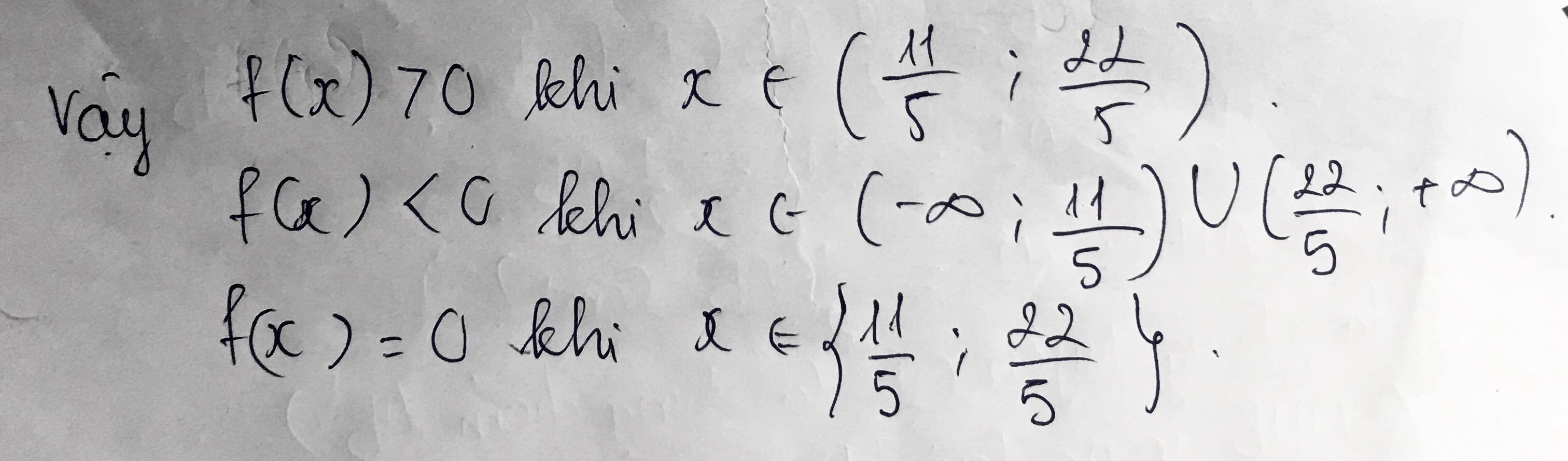
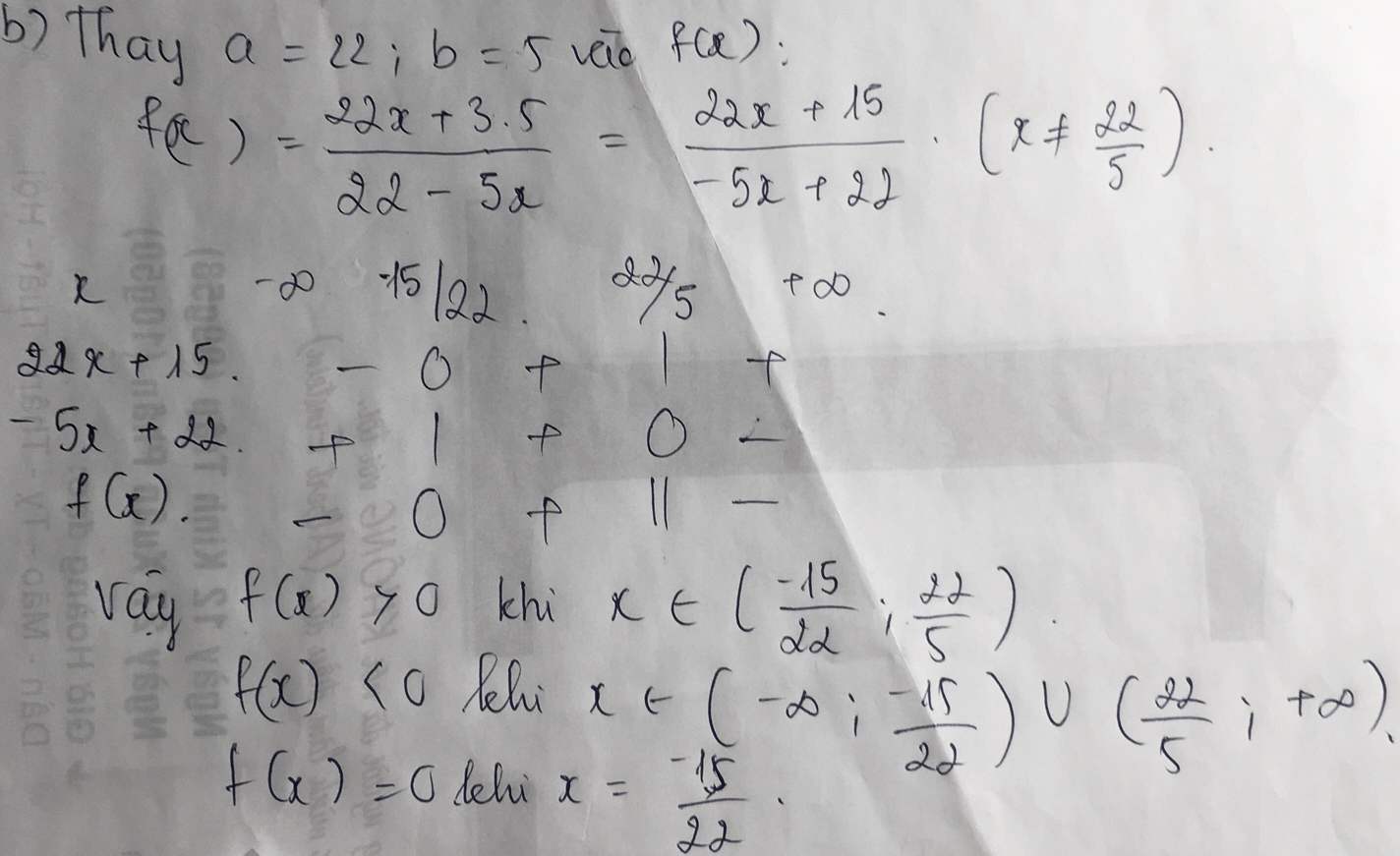

a: 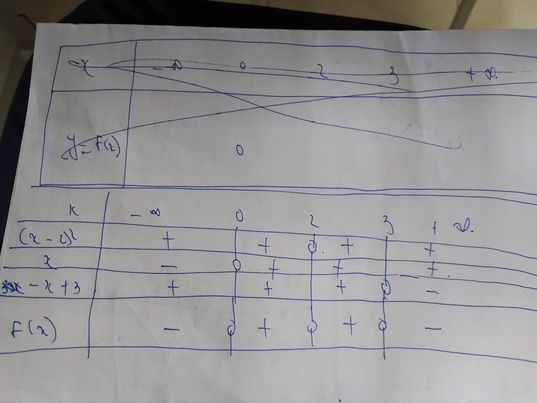
b: 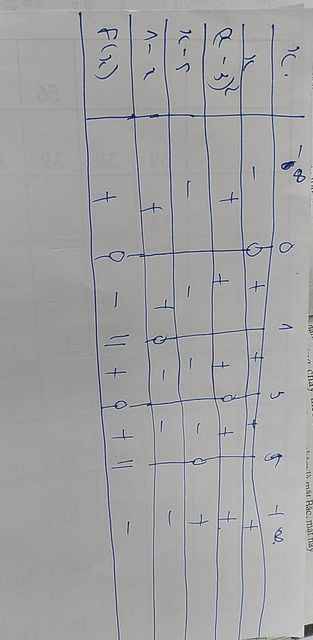
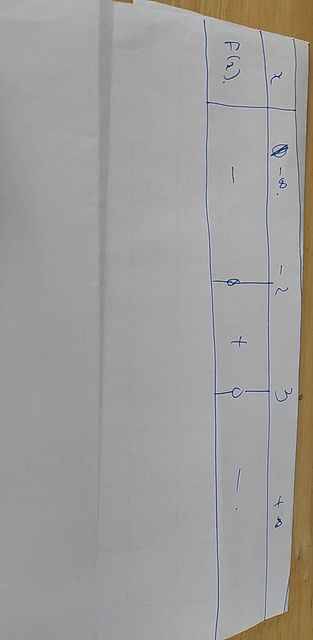
c: Đặt f(x)=0
=>-x^2+x+6=0
=>x^2-x-6=0
=>x=3 hoặc x=-2
d: 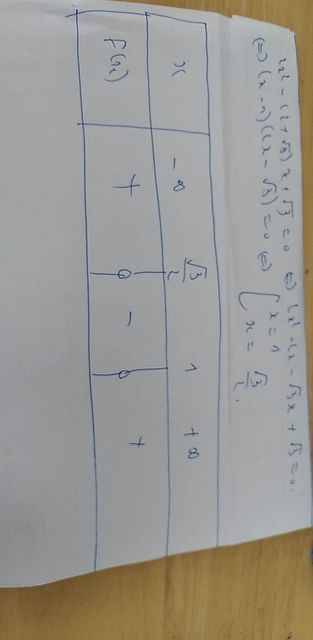

Mệnh đề đảo là : "Nếu \(f\left(x\right)\) có một nghiệm bằng 1 thì \(a+b+c=0\)". "Điều kiện cần và đủ để \(f\left(x\right)=ax^2+bx+c\) có một nghiệm bằng 1 là \(a+b+c=0\)"

\(\Delta=b^2-4ac\le0\Rightarrow b^2\le4ac\Rightarrow\frac{a}{b}.\frac{c}{b}\ge\frac{1}{4}\)
Đặt \(\left(\frac{a}{b};\frac{c}{b}\right)=\left(x;y\right)\Rightarrow xy\ge\frac{1}{4}\)
\(F=4x+y\ge4\sqrt{xy}\ge4\sqrt{\frac{1}{4}}=2\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}x=\frac{1}{4}\\y=1\end{matrix}\right.\) hay \(b=c=4a\)

a) f(x) = (x+2)(x-1)
f(x) > 0 với x < -2 hoặc x > 1
f(x) ≤ 0 với -2 ≤ x ≤ 1
b) y = 2x (x + 2) = 2(x+1)2 – 2
Bảng biến thiên:
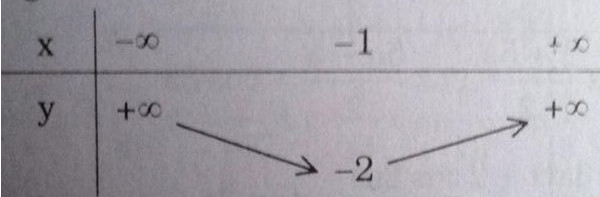
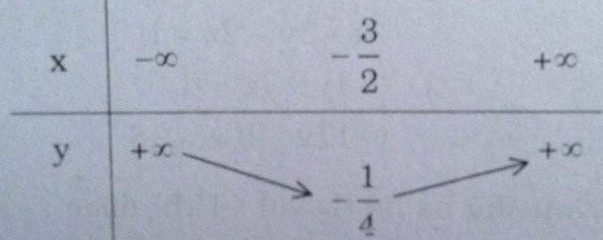
Hàm số : y = \(\left(x+2\right)\left(x+1\right)=\left(x+\dfrac{3}{2}\right)^2-\dfrac{1}{4}\)
Bảng biến thiên :
Đồ thị (C1) và (C2)
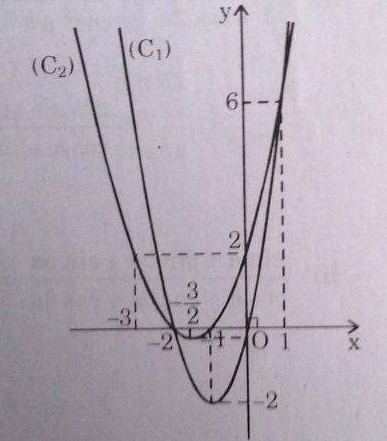
Hoành độ các giao điểm A và B của (C1) và (C2) là nghiệm của phương trình f(x) = 0 ⇔ x1 = -2, x2 = 1
⇔ A(-2, 0) , B(1, 6)
c) Giải hệ phương trình
\(\left\{{}\begin{matrix}\dfrac{ac-b^2}{4a}\\a\left(-2\right)^2+b\left(-2\right)+c=0\\a\left(1\right)^2+b\left(1\right)+c=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2,b=0,c=8\\a=-\dfrac{2}{9},b=\dfrac{16}{9},c=\dfrac{40}{9}\end{matrix}\right.\)