Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
đúng và khẳng định 
sai.
sai và khẳng định 
đúng.
sai và khẳng định 
sai.
đúng và khẳng định 
đúng.
Chọn D
Trong khoảng 
đồ thị hàm số y= f’(x) nằm phía trên trục hoành nên hàm số y= f( x) đồng biến trên khoảng ( 0; π)
Chọn D
Ta có
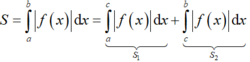
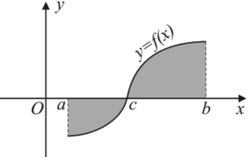
Vì f(x) < 0, ∀ x ∈ a ; c nên |f(x)| = –f(x).
Do đó, S 1 = - ∫ a c f x d x .
Tương tự, f(x) > 0, ∀ x ∈ a ; c nên |f(x)| = f(x).
Do đó, S 2 = ∫ c b f x d x .
Vậy S = - ∫ a c f x d x + ∫ c b f x d x .
Chọn D
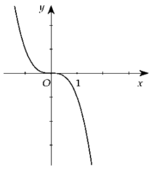
Trong khoảng (0 ; + ∞) đồ thị hàm số y= f’( x) nằm phía dưới trục hoành- tức là f’( x)< 0 trên khoảng đó
=> Hàm số y= f(x) nghịch biến trên khoảng 
Chọn C
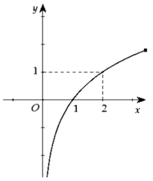
Trong khoảng ( 0; 1) đồ thị hàm số y= f’( x) nằm phía dưới trục hoành nên trên khoảng này thì f’( x)< 0.
=> hàm số f(x) nghịch biến trên khoảng (0; 1) .
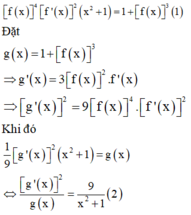
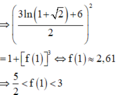
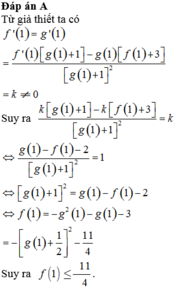
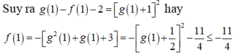
Đáp án C
Cả hai khẳng định đều sai vì thiếu điều kiện hàm số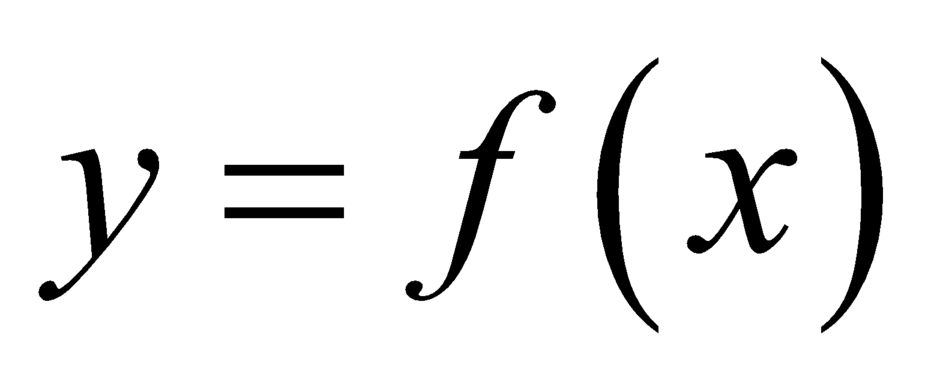
liên tục.