Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

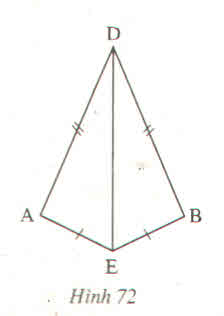
a) Xét \(\Delta ADE;\Delta BDE:\)
AD = BD (gt)
ED chung
AE = BE (gt)
\(\Rightarrow\Delta ADE=\Delta BDE\left(c.c.c\right)\)
b) Vì \(\Delta ADE=\Delta BDE\) (câu a)
nên \(\widehat{DAE}=\widehat{DBE}\) (2 góc t/ư).
Xem hình vẽ:
a) ∆ADE và ∆BDE có
DE cạnh chung
AD=DB(gt)
AE=BE(gt)
Vậy ∆ADE=∆BDE(c.c.c)
b) Từ ∆ADE=∆BDE(cmt)
Suy ra \(\widehat{DAE}\)=\(\widehat{DBE}\)(Hai góc tương ứng)

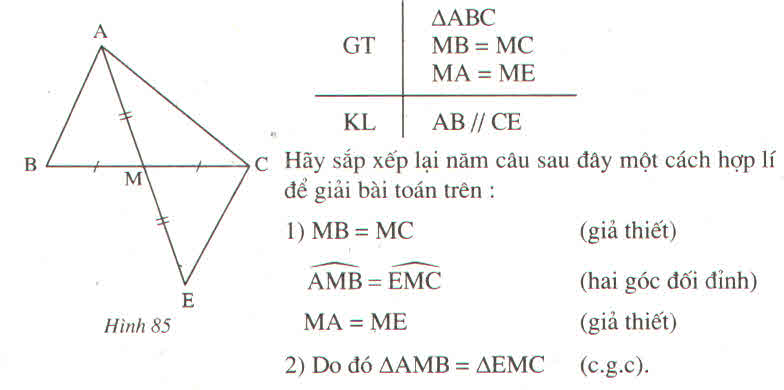
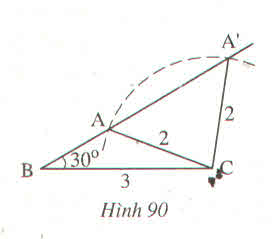
Góc ABC không phải là góc xen giữa BC và CA, Góc A'BC không phải là góc xen giữa hai cạnh BC và CA'. Do đó không thể sử dụng trường hợp cạnh góc cạnh để kết luận ∆ABC=∆A'B 'C' được.
Góc ABC không phải là góc xen giữa BC và CA, Góc A'BC không phải là góc xen giữa hai cạnh BC và CA'. Do đó không thể sử dụng trường hợp cạnh góc cạnh để kết luận ∆ABC=∆A'B 'C' được.

A B C N M y x 1 2 1
a) Vì AM là phân giác của góc BAM
=> Góc A1 = góc A2
Mà góc A1 = góc M1 ( do AB // MN )
=> Góc A2 = góc M1 ( điều phải c/m )
b) Vì Bx là phân giác góc ABC => Góc NBM = 1/2 góc ABC
Vì My là p/g của góc NMC => Góc yMC = 1/2 góc NMC
Mà góc NMC = góc ABC ( do AB // MN )
=> Điều phải c/m
c) Bn tự làm nốt nha
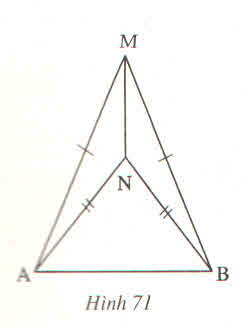



Xét tg AMN và tg BMN có:
MN chung
MA = MB (gt)
NA = NB (gt)
=> tg AMN = tg BMN (c.c.c)
1) Giả thiết: \(\Delta AMN;\Delta BMN\) có: MA = MB và NA = NB.
Kết luận: tg AMN = tg BMN
2) \(\Delta AMN\) và \(\Delta BMN\) có:
MN: cạnh chung
MA = MB (giả thiết)
NA = NB (giả thiết)
Do đó \(\Delta AMN=\Delta BMN\left(c.c.c\right)\)
Suy ra \(\widehat{AMN}=\widehat{BMN}\) (2 góc t/ư).
bạn làm sai chỗ Kết luận: tg AMN = tg BMN VÌ ngta nói chứng minh góc chứ ko phải tg