Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

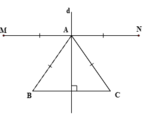
Ta có: B A M ^ = B ^ ( g t ) C A N ^ = C ^ ( g t )
Þ AM // BC; AN // BC (vì có cặp góc so le trong bằng nhau).
Þ 3 điểm M, A, N thẳng hàng (vì qua điểm A chỉ vẽ được một đường thẳng song song với BC).
Vậy MN // BC mà d ⊥ B C nên d ⊥ M N (1)
Ta có: A M = A B ; A N = A C
mà AB = AC (gt) nên AM = AN. (2)
Từ (1) và (2) Þ d là trung trực của MN

Bài 1:
a: Ta có: \(\hat{BAD}+\hat{BAC}=\hat{DAC}=90^0\)
\(\hat{EAC}+\hat{BAC}=\hat{EAB}=90^0\)
Do đó: \(\hat{BAD}=\hat{EAC}\)
Xét ΔBAD và ΔEAC có
BA=EA
\(\hat{BAD}=\hat{EAC}\)
AD=AC
Do đó: ΔBAD=ΔEAC
=>BD=EC
b: Xét ΔMAB và ΔMNC có
MA=MN
\(\hat{AMB}=\hat{NMC}\) (hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMNC
=>AB=NC
mà AB=AE
nên CN=AE
ΔMAB=ΔMNC
=>\(\hat{MAB}=\hat{MNC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//NC
=>\(\hat{ACN}+\hat{BAC}=180^0\) (1)
Ta có: \(\hat{DAE}+\hat{BAC}\)
\(=\hat{DAB}+\hat{BAC}+\hat{CAE}+\hat{BAC}\)
\(=2\cdot\hat{DAB}+2\cdot\hat{BAC}=2\left(\hat{DAB}+\hat{BAC}\right)=2\cdot\hat{DAC}=180^0\) (2)
Từ (1),(2) suy ra \(\hat{ACN}=\hat{DAE}\)
Xét ΔACN và ΔDAE có
AC=DA
\(\hat{ACN}=\hat{DAE}\)
CN=AE
Do đó: ΔACN=ΔDAE
c: ΔACN=ΔDAE
=>\(\hat{CAN}=\hat{ADE}\)
mà \(\hat{CAN}+\hat{DAN}=\hat{DAC}=90^0\)
nên \(\hat{ADE}+\hat{DAN}=90^0\)
=>AN⊥DE tại I
=>ΔAID vuông tại I; ΔAIE vuông tại I
ΔAID vuông tại I
=>\(AD^2=AI^2+ID^2\)
ΔAIE vuông tại I
=>\(AE^2=AI^2+IE^2\)
\(\frac{AD^2+IE^2}{DI^2+AE^2}=\frac{AI^2+ID^2+IE^2}{DI^2+AI^2+IE^2}=1\)
Bài 2:
a: Ta có: \(\hat{BAH}+\hat{CAH}=\hat{BAC}=90^0\)
\(\hat{CAH}+\hat{ACI}=90^0\) (ΔAIC vuông tại I)
Do đó: \(\hat{ICA}=\hat{HAB}\)
Xét ΔICA vuông tại I và ΔHAB vuông tại H có
CA=AB
\(\hat{ICA}=\hat{HAB}\)
Do đó: ΔICA=ΔHAB
=>AI=BH
b: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là phân giác của góc BAC
=>\(\hat{BAM}=\frac12\cdot\hat{BAC}=45^0\)
ΔBAC vuông cân tại A
=>\(\hat{ACB}=45^0\)
=>\(\hat{ACM}=\hat{BAM}\)