Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đề nghị khi đăng câu hỏi nên ấn 1 lần, sau ns sẽ hiện ra, tốn S ==

Câu 1:
Khong gian mẫu: \(C_{11}^3\)
Có 5 cặp bi cùng số, do đó có \(5\) cách chọn ra 1 cặp cùng số, viên còn lại có 9 cách chọn \(\Rightarrow\) có 45 cách chọn 3 viên có 2 viên cùng số (tất nhiên là ko thể 3 viên cùng số được)
Xác suất: \(P=\frac{C_{11}^3-45}{C_{11}^3}=\frac{8}{11}\)
Câu 2:
Không gian mẫu: \(9!\)
Xếp 4 bạn nam cạnh nhau và hoán vị, có \(4!\) cách
Coi 4 bạn nam này là 1 người, xếp hàng cùng 5 bạn nữ \(\Rightarrow\) có \(6!\) cách hoán vị
Vậy có \(4!.6!\) cách
Xác suất: \(P=\frac{4!.6!}{9!}=\frac{1}{21}\)

Số tự nhiên thỏa mãn có dạng với a,b,c,d ∈ A và đôi một khác nhau.
TH1: d=0
Có 5 cách chọn a; 4 cách chọn b và 3 cách chọn c nên theo quy tắc nhân có 5.4.3 = 60 số.
TH2: d ≠ 0 ; d có 2 cách chọn là 2, 4
Khi đó có 4 cách chọn a( vì a khác 0 và khác d); có 4 cách chọn b và 3 cách chọn c.
Theo quy tắc nhân có: 2.4.4.3=96 số
Vậy có tất cả: 96 + 60 = 156 số.

gọi số cần tìm là abcdef (a#0 ; a;b;c;d;e;f € A ; f chẵn )
f có 3 cách chọn
a có 5 cách chọn lọc
b;c;d;e đều có 6 cách chọn
=> có 3*5*6*6*6*6 = 19440 số thỏa mãn yêu cầu bài toán
b) gọi số cần tìm là abcdef (a#0;f=0,5 ; a;b;c;d;e;f € A )
f=0,5 => f có 2 cách chọn
a có 5 cách chọn
b;c;d;e đều có 6 cách chọn
=> có 2*5*6*6*6*6 = 12960
Bước 1: Xếp 3 bi đỏ khác nhau vào hộp có 7 ô trống có cách.
Bước 2: Xếp 3 bi xanh vào 4 ô trống còn lại,có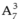 cách.
cách.
Theo quy tắc nhân ta có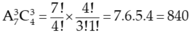 cách.
cách.
Chọn C.