Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

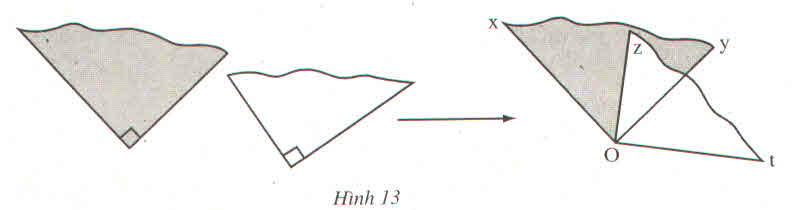
b) Có: \(\widehat{xOz}+\widehat{yOz}=\widehat{yOz}+\widehat{yOt}=90^o\)
\(\Rightarrow\widehat{xOz}=\widehat{yOt}\)(cùng phụ \(\widehat{yOz}\))
c)Gọi Om là tia p/g \(\widehat{yOz}\).
Có: \(\widehat{xOz}+\widehat{zOm}=\widehat{mOy}+\widehat{yOt}\)(Vì \(\widehat{xOz}=\widehat{yOt};\widehat{zOm}=\widehat{mOy}\))
\(\Rightarrow\widehat{xOm}=\widehat{mOt}\)
\(\Rightarrow\)Om là tia p/g của \(\widehat{xOt}\).

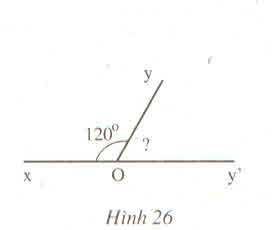
ta có : xOy va yOy' la hai goc ke nhau
=) xOy = 180 do
=> yOy' + xOy = xOy'
=> yOy' = xOy' - xOy =180 - 120 = 60 do
vay yOy' = 60 do

a,b:
| Tên góc | Số đo ước lượng | Số đo bằng thước |
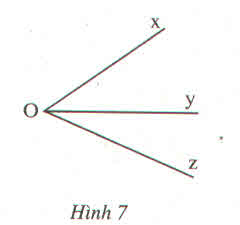
| góc xAy | 20 độ | 23 độ |
| góc zBt | 60 độ | 53 độ |
| góc sDr | 120 độ | 128 độ |
| góc mCn | 100 độ | 106 độ |
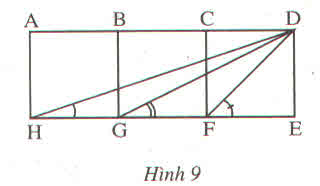
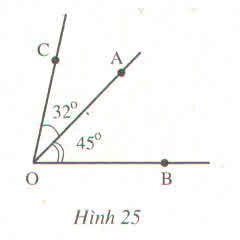
| góc BAC | 30 độ | 30 độ |
| góc BDC | 45 độ | 45 độ |
| góc ACD | 100 độ | 105 độ |
| góc BCD | 45 độ | 45 độ |
| góc BCA | 60 độ | 60 độ |
| góc ABC | 90 độ | 90 độ |
| góc CBD | 90 độ | 90 độ |
c: \(\widehat{xAy}< \widehat{BAC}< \widehat{BDC}=\widehat{BCD}< \widehat{zBt}< \widehat{BCA}< \widehat{ABC}=\widehat{CBD}< \widehat{ACD}< \widehat{mCn}< \widehat{sDr}\)

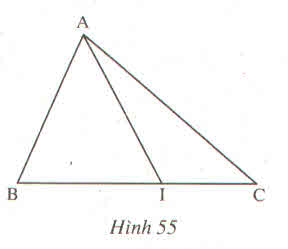
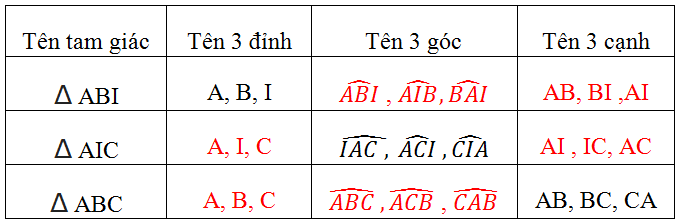
Giải:
|
Tên tam giác |
Tên 3 đỉnh |
Tên 3 góc |
Tên 3 cạnh |
|
|
A,B,I |
|
AB, BI, IA |
|
|
A,I,C |
|
AI, IC, CA |
|
|
A,B,C |
|
AB, BC, CA |
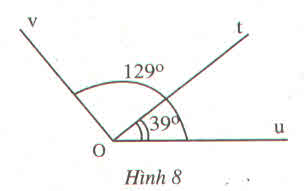





Theo hình vẽ, ta có: \(\widehat{uOt}+\widehat{tOv}=\widehat{uOv}\\ =>\widehat{tOv}=\widehat{uOv}-\widehat{uOt}\\ \widehat{tOv}=129^o-39^o=90^o\)
Với: \(\widehat{tOv}=90^o\)
=> \(\widehat{tOv}\) là góc vuông