Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Trên hình có 3 góc, đó là các góc xOy;yOz; xOz
b: Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOy}< \widehat{xOz}\)
nên tia Oy nằm giữa hai tia Ox và Oz
mà \(\widehat{xOy}=\dfrac{1}{2}\widehat{xOz}\)
nên Oy là phân giác của góc xOz
c: \(\widehat{zOx'}=180^0-120^0=60^0\)

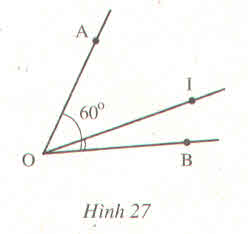
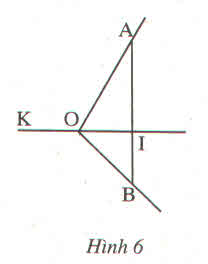
\(\widehat{BOI}\) = \(\dfrac{1}{4}\) \(\widehat{AOB}\) ⇒ \(\dfrac{1}{4}\).60o = 15o
Vì tia OI nằm giữa 2 tia OA; OB nên:
\(\widehat{AOI}\)+ \(\widehat{IOB}\)= \(\widehat{AOB}\)
⇒ \(\widehat{AOI}\)= \(\widehat{AOB} - \widehat{IOB}\) = 60o - 15o = 45o
Vậy: \(\widehat{AOI}\) = 45o

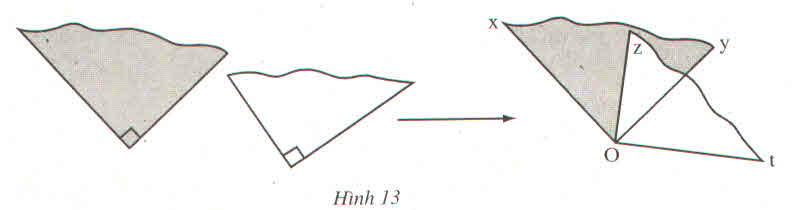
b) Có: \(\widehat{xOz}+\widehat{yOz}=\widehat{yOz}+\widehat{yOt}=90^o\)
\(\Rightarrow\widehat{xOz}=\widehat{yOt}\)(cùng phụ \(\widehat{yOz}\))
c)Gọi Om là tia p/g \(\widehat{yOz}\).
Có: \(\widehat{xOz}+\widehat{zOm}=\widehat{mOy}+\widehat{yOt}\)(Vì \(\widehat{xOz}=\widehat{yOt};\widehat{zOm}=\widehat{mOy}\))
\(\Rightarrow\widehat{xOm}=\widehat{mOt}\)
\(\Rightarrow\)Om là tia p/g của \(\widehat{xOt}\).

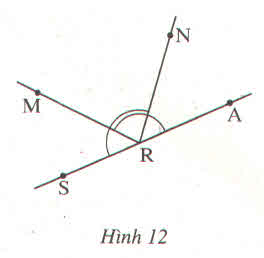
b: \(\widehat{MRS}=180^0-130^0=50^0\)
\(\widehat{ARN}=180^0-130^0=50^0\)
\(\widehat{MRN}=180^0-50^0-50^0=80^0\)

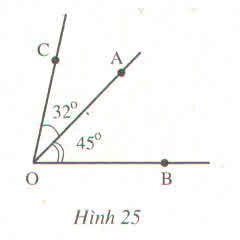
\(\widehat{AOI}=180^0-120^0=60^0\)
\(\widehat{KOB}=180^0-45^0=135^0\)
\(\widehat{BOA}=60^0+45^0=105^0\)

Giải:
Có thể vẽ hình như sau:
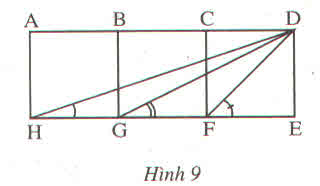
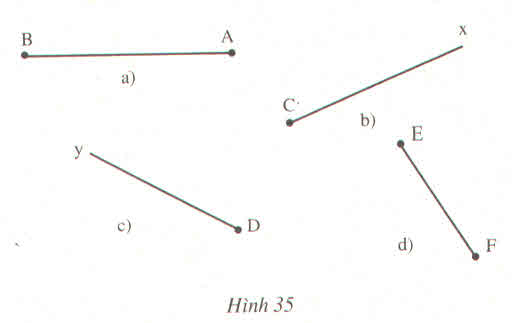
a) Đỉnh của góc là A, một cạnh là AB, cần vẽ tia AC.
b) Đỉnh của góc là C, một cạnh là Cx, cần vẽ tia Cz.
c) Đỉnh của góc là D, một cạnh là Dy, cần vẽ tia Dx.
d) Đỉnh của góc là F, Một cạnh là EF, cần vẽ tia Fy.


3 tia chung gốc:
O x y z 1 2 3