Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

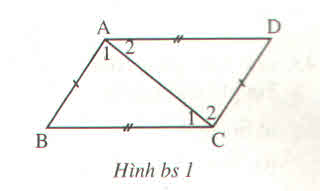
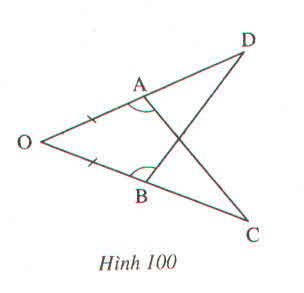
\(\widehat{A}_1=\widehat{C}_2;\widehat{A}_2=\widehat{C}_1;\widehat{B}=\widehat{D}\)

đây là cậu chép trg chỗ giải đáp rồi mà mk ko đc lm giống trg giải đáp

GT: DI là tia phân giác của \(\widehat{MDN}\)
\(\widehat{EDK}\) đối đỉnh với \(\widehat{IDM}\)
KL: \(\widehat{EDK}=\widehat{IDM}\)
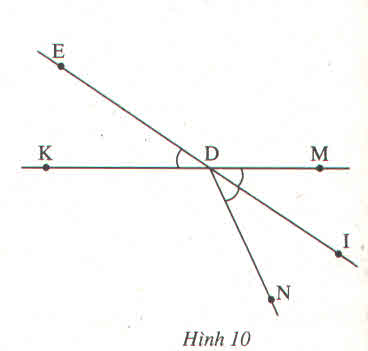
Chứng minh (h.10)
ˆIDM=ˆIDNIDM^=IDN^ (vì DI là tia phân giác của \(\widehat{MDN}\)) (1)
ˆIDM=ˆEDKIDM^=EDK^ (vì 2 góc này đối đỉnh) (2)
Từ (1) và (2) suy ra \(\widehat{EDK}=\widehat{IDN}\)

a) Xét \(\Delta ADE;\Delta BDE:\)
AD = BD (gt)
ED chung
AE = BE (gt)
\(\Rightarrow\Delta ADE=\Delta BDE\left(c.c.c\right)\)
b) Vì \(\Delta ADE=\Delta BDE\) (câu a)
nên \(\widehat{DAE}=\widehat{DBE}\) (2 góc t/ư).
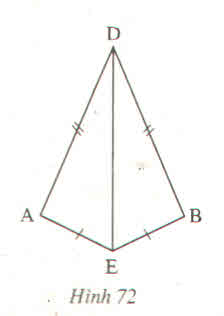
Xem hình vẽ:
a) ∆ADE và ∆BDE có
DE cạnh chung
AD=DB(gt)
AE=BE(gt)
Vậy ∆ADE=∆BDE(c.c.c)
b) Từ ∆ADE=∆BDE(cmt)
Suy ra \(\widehat{DAE}\)=\(\widehat{DBE}\)(Hai góc tương ứng)

|
Câu |
Đúng |
Sai |
|
1.Trong một tam giác, góc nhỏ nhất là góc nhọn |
x |
|
|
2.Trong một tam giác, có ít nhất là hai góc nhọn |
x |
|
|
3.Trong một tam giác, góc lớn nhất là góc tù |
|
x |
|
4.Trong một tam giác vuông, hai góc nhọn bù nhau |
|
x |
|
5. Nếu ˆAA^ là góc ở đáy của một tam giác cân thì ˆAA^ < 900 |
x |
|
|
6.Nếu ˆAA^ là góc ở đỉnh của một tam giác cân thì ˆAA^ < 900 |
|
x |

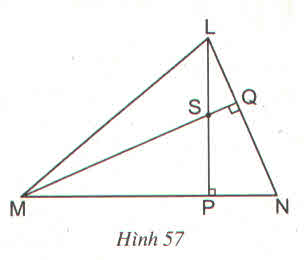
a) Từ hình vẽ ta có: LP ⊥ MN; MQ ⊥ LN
ΔMNL có S là giao điểm của hai đường cao LP và MQ nên S chính là trực tâm của tam giác (định lí ba đường cao).
=> NS cũng là đường cao trong tam giác hay NS ⊥ LM (đpcm).
b) ΔNMQ vuông tại Q có góc LNP = 50o nên góc QMN = 40o
ΔMPS vuông tại P có góc QMP = 40o nên góc MSP = 50o
Vì hai góc MSP và PSQ là hai góc kề bù nên suy ra:
góc PSQ = 180o - 50o = 130o.
Hướng dẫn:
a) Trong ∆NML có :
LP ⊥ MN nên LP là đường cao
MQ ⊥ NL nên MQ là đường cao
mà PL ∩ MQ = {S}
suy ra S là trực tâm của tam giác nên đường thằng SN chứa đường cao từ N hay
SN ⊥ ML
b) ∆NMQ vuông tại Q có ˆLNPLNP^ =500 nên ˆQMNQMN^ =400
∆MPS vuông tại Q có ˆQMPQMP^ =400 nên ˆMSPMSP^ =500
Suy ra ˆPSQPSQ^ =1300(kề bù)









GT Hai góc đối đỉnh
KL bằng nhau