Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi A là biến cố "sản phẩm chọn được từ lô 2 là loại A"
\(B_1\) là biến cố "viên bi được lấy ra là viên của hộp 1" \(\Rightarrow P\left(B_1\right)=\dfrac{C_5^1}{C_{20}^1}=\dfrac{1}{4}\)
\(B_2\) là biến cố "viên bi được lấy ra là viên bi của hộp 2" \(\Rightarrow P\left(B_2\right)=\dfrac{C_{15}^1}{C_{20}^1}=\dfrac{3}{4}\)
\(P\left(A|B_1\right)=\dfrac{C_3^1}{C_7^1}=\dfrac{3}{7}\)
\(P\left(A|B_2\right)=\dfrac{C_9^1}{C_{15}^1}=\dfrac{3}{5}\)
Xác suất:
\(P\left(A\right)=\dfrac{1}{4}.\dfrac{3}{7}+\dfrac{3}{4}.\dfrac{3}{5}=\dfrac{39}{70}\)

Chọn A.
Gọi x; y lần lượt là số phẩm loại A; B.
Theo đề bài ta có: 2000x + 4000y = 40 000 hay x + 2y = 20
Suy ra: x = 20 - 2y.
Ta có ![]()
Xét hàm ![]()
Tập xác định D = (0; 10).
![]()
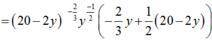
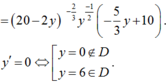
Nhận xét: ![]() nên dấu của y’ là dấu của biểu thức
nên dấu của y’ là dấu của biểu thức ![]()
Do đó hàm số đạt giá trị lớn nhất khi y = 6 và x = 8
Vậy ![]()



Gọi \(A_1\) là biến cố: "2 sản phẩm lấy nhầm từ lô 1 đều là sản phẩm tốt"
\(A_2\) là biến cố: "2 sản phẩm lấy nhầm từ lô 1 có 1 sản phẩm tốt 1 sản phẩm xấu"
`A_3` là biến cố: "2 sản phẩm lấy nhầm từ lô 1 đều là sản phẩm xấu"
\(\Rightarrow P\left(A_1\right)=\dfrac{C_6^2}{C_9^2}=\dfrac{5}{12}\); \(P\left(A_2\right)=\dfrac{C_6^1.C_3^1}{C_9^2}=\dfrac{1}{2}\); \(P\left(A_3\right)=\dfrac{C_3^2}{C_9^2}=\dfrac{1}{12}\)
\(A_1;A_2;A_3\) tạo thành 1 nhóm biến cố đầy đủ
Gọi B là biến cố: "sản phẩm cuối cùng lấy ra là sản phẩm tốt"
\(\Rightarrow P\left(B|A_1\right)=\dfrac{5+2}{7+2}=\dfrac{7}{9}\);
\(P\left(B|A_2\right)=\dfrac{5+1}{7+2}=\dfrac{2}{3}\);
\(P\left(B|A_3\right)=\dfrac{5}{7+2}=\dfrac{5}{9}\)
a.
\(P\left(B\right)=P\left(A_1\right).P\left(B|A_1\right)+P\left(A_2\right).P\left(B|A_2\right)+P\left(A_3\right).P\left(B|A_3\right)\)
\(=\dfrac{5}{12}.\dfrac{7}{9}+\dfrac{1}{2}.\dfrac{2}{3}+\dfrac{1}{12}.\dfrac{5}{9}=\dfrac{19}{27}\)
b.
Gọi `C_1` là biến cố "sản phẩm cuối cùng lấy ra thuộc lô 1"
`C_2` là biến cố: "sản phẩm cuối cùng lấy ra thuộc lô 2"
\(\Rightarrow P\left(C_1\right)=\dfrac{2}{9};P\left(C_2\right)=\dfrac{7}{9}\)
`C_1`, `C_2` cũng là nhóm biến cố đầy đủ
\(P\left(B|C_1\right)=\dfrac{6}{9}=\dfrac{2}{3}\)
\(\Rightarrow P\left(C_1|B\right)=\dfrac{P\left(B|C_1\right).P\left(C_1\right)}{P\left(B\right)}=\dfrac{\dfrac{2}{3}.\dfrac{2}{9}}{\dfrac{19}{27}}=\dfrac{4}{19}\)
c.
\(P\left(A_2|B\right)=\dfrac{P\left(B|A_2\right).P\left(A_2\right)}{P\left(B\right)}=\dfrac{\dfrac{2}{3}.\dfrac{1}{2}}{\dfrac{19}{27}}=\dfrac{9}{19}\)