Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Lấy quyển đầu tiên là Văn trong 9 quyển Văn có C 9 1 cách
Lấy quyển đầu tiên là Văn trong 8 quyển Văn có C 8 1 cách
Lấy quyển đầu tiên là Anh trong 6 quyển Anh có C 6 1 cách
Suy ra số kết quả thuận lợi của biến cố là n(X) = 9.8.6 = 432
Vậy xác suất cần tính là
P = n ( X ) n ( Ω ) = 432 15 . 14 . 13 = 72 455 .

Chọn D
Số phần tử không gian mấu bằng số cách lấy ra 4 sản phẩm từ 20 sản phẩm là: C 20 4 (cách)
Cách 1: Để lấy ra 4 sản phẩm có sản phẩm lỗi ta chia các trường hợp:
TH1: Lấy được 3 sản phẩm tốt và 1 sản phẩm lỗi, ta có: C 18 3 . C 2 1 (cách)
TH2: Lấy được 2 sản phẩm tốt và 2 sản phẩm lỗi, ta có: C 18 2 . C 2 2 (cách)
Vậy xác suất cần tìm là: 
Cách 2: Xét biến cố đối:
Số cách lấy ra 4 sản phẩm không có sản phẩm lỗi C 18 4 (cách)
Vậy xác suất cần tìm là: 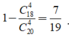

Đáp án C
Phương pháp giải: Sử dụng biến cố đối và các quy tắc đếm cơ bản.
Lời giải:
Chọn 3 quyển sách trong 15 quyển sách có C 15 3 = 455 cách ⇒ n ( Ω ) = 455
Gọi X là biến cố 3 quyển sách được lấy ra có ít nhất một quyển sách là toán.
Và X là biến cố 3 quyển sách được lấy ra không có quyển sách toán. Khi đó, ta xét các trường hợp sau:
TH1. Lấy được 2 quyển lý, 1 quyển hóa => có C 5 2 . C 6 1 = 60 cách
TH2. Lấy được 1 quyển lý, 2 quyển hóa => có C 5 1 . C 6 2 = 75 cách
TH3. Lấy được 3 quyển lý, 0 quyển hóa => có C 5 3 . C 6 0 = 10 cách
TH4. Lấy được 0 quyển lý, 3 quyển hóa => có C 5 0 . C 6 3 = 20 cách
Suy ra số phần tử của biến cố X là
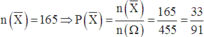
Vậy xác suất cần tính là
![]()

Đáp án A
Tổng số quyển sách trên giá là: 4 + 3 + 2 = 9 (quyển).
Số cách lấy ra 3 quyển sách từ 9 quyển sách đó là: C 9 3 .
Số cách lấy ra 3 quyển sách trong đó không có quyển sách toán nào là: C 5 3 .
Xác suất để 3 quyển được lấy ra có ít nhất một quyển là toán là C 9 3 - C 5 3 C 9 3 = 37 42

Đáp án C
Lấy ngẫu nhiên 3 cuốn sách có: C 9 3 = 84 cách
Gọi A là biến cố:
Lấy 3 cuốn sách và không có cuốn nào là cuốn toán
Suy ra A ¯ là biến cố:
3 quyển được lấy ra có ít nhất một quyển là toán
Khi đó Ω A = C 5 3 = 10
Vậy P A = Ω A Ω = 5 42
⇒
p
A
¯
=
1
-
p
A
=
37
42

Đáp án C
Phương pháp.
Sử dụng định nghĩa của xác suất.
Lời giải chi tiết.
Tổng số sách là 4 + 3 + 2 = 9. Số cách lấy 3 quyển sách là C 9 3 = 84 (cách).
Số quyển sách không phải là sách toán là 3 + 2 = 5
Số cách lấy 3 quyển sách không phải là sách toán là C 5 3 = 10 (cách).
Do đó số cách lấy được ít nhất một quyển sách toán là 84 - 10 = 74 (cách).
Vậy xác suất để lấy đượcc ít nhất một quyển là toán là 74 84 = 37 42

Nếu bạn mới học lớp 11 thì không cần quan tâm bài xác suất này.
Đây là xác suất phân phối của biến rời rạc nằm trong chương trình xác suất thống kê của đại học, phương pháp tính riêng (cần có bảng để tra) hoàn toàn ko liên quan đến xác suất của phổ thông
Lời giải:
Xác suất để quyển sách không lỗi trang nào:
\((1-0,002)^{1000}\)
Xác suất để quyển sách lỗi 1 trang:
\((1-0,002)^{999}.0,002.1000=2.0,998^{999}\)
Xác suất để quyển sách lỗi 2 trang là:
\((1-0,002)^{998}.0,002^2.C^2_{1000}\)
Cộng ba số trên ta có xác suất cần tìm.