Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hoành độ giao điểm của hai đồ thị thỏa mãn pt : \(x^2=-x+2\Leftrightarrow x^2+x-2=0\)
Giải ra ta được x1 , x2 .Thay x1 ,x2 vừa tìm được vào một trong hai công thức hàm số,ta được y1,y2.

chào ng đẹp
a) tự vẽ
b) pt hoành độ 1/2x^2=3/2x-1
Giải pt bậc 2 ra có x1=..;x2=..
thay lần lượt x1=...;x2=.... vô y=1/2x^2
ta dc y1=..;y2=...
ta được 2 giao điểm của (P) và (d) là A(x1;y1);B(x2;y2)
a,y=1/2x2
bạn lập bảng giá trị :
| x | -2 | -1 | 0 | 1 | 2 |
| y | 2 | 1/2 | 0 | 1/2 | 2 |
sau đó thay vào vẽ parabol .
b,vì là giao điểm của (P) và (d) nên suy ra :
\(\frac{1}{2}\)x2= \(\frac{3}{2}\)x-1
chuyển thành pt bậc 2 và giải ta đk kết quả của x là hoành độ , y là tung độ của giao điểm
chúc bạn học tập tốt phần này vì nó là kiến thức quan trọng cho th vào lớp 10

1) Xác định được ít nhất hai điểm phân biệt thuộc đường thẳng d. Chẳng hạn: A ( − 3 ; 0 ) ; B ( 0 ; 3 ) .
Xác định được đỉnh và ít nhất hai điểm thuộc (P) . Chẳng hạn : O ( 0 ; 0 ) ; C ( 6 ; 9 ) ; E ( − 6 ; 9 ) .
Đồ thị
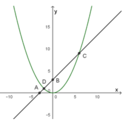
2) Phương trình hoành độ giao điểm: 1 4 x 2 = x + 3 ⇔ 1 4 x 2 − x − 3 = 0 ⇔ x = − 2 hoặc x= 6
Tọa độ giao điểm là D ( − 2 ; 1 ) v à C ( 6 ; 9 ) .

giúp mình đi vẽ hộ cái hình
cho đường tròn tâm O bán kính r,điểm A cố định nằm ngoài đường tròn.kẻ 2 tiếp tuyến AM,AN.Đường thẳng D đi qua A cắt đường tròn O tại B,C với AB<AC.Chứng minh 5 điểm A,M,N,O,I thuộc đường tròn

a: Thay x=2 vào (P),ta được:
y=2^2/2=2
2: Thay x=2 và y=2 vào (d), ta được:
m-1+2=2
=>m-1=0
=>m=1

1. PT hoành độ giao điểm:
x2−(2x−m2+9)=0⇔x2−2x+m2−9=0(∗)
Khi m=1
thì pt trên trở thành: x2−2x−8=0
⇔(x−4)(x+2)=0⇒x=4
hoặc x=−2
Khi x=4⇒y=x2=16
. Giao điểm thứ nhất là (4,16)
Khi x=−2⇒y=x2=4
. Giao điểm thứ hai là (−2,4)
2. (P)
và (d) cắt nhau tại 2 điểm phân biệt ⇔(∗)
có 2 nghiệm phân biệt (hai nghiệm ấy chính là giá trị của 2 hoành độ giao điểm)
⇔Δ′=1−(m2−9)>0⇔10>m2(1)
Hai giao điểm nằm về phía của trục tung, nghĩa là 2 hoành độ giao điểm x1,x2
trái dấu. Điều này xảy ra khi x1x2<0⇔m2−9<0(2)
Từ (1);(2)
suy ra m2−9<0⇔−3<m<3
Phương trình hoành độ giao điểm là:
\(x^2-x\sqrt{3}+\sqrt{3}-1=0\)
\(\text{Δ}=\left(\sqrt{3}\right)^2-4\cdot1\cdot\left(\sqrt{3}-1\right)=3-4\sqrt{3}+4=7-4\sqrt{3}=\left(2-\sqrt{3}\right)^2\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{\sqrt{3}-2+\sqrt{3}}{2}=\sqrt{3}-1\\x_2=\dfrac{\sqrt{3}+2-\sqrt{3}}{2}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y_1=4-2\sqrt{3}\\y_2=1\end{matrix}\right.\)