Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Biến thiên động lượng:
\(\Delta p=m\left(v_1-v_2\right)=0,025\cdot\left(800-0\right)=20kg.m\)/s
Mà \(\Delta p=F\cdot t\)
\(\Rightarrow F=\dfrac{\Delta p}{t}=\dfrac{20}{2,5}=8N\)

Động lượng viên đạn bay ra khỏi nòng:
\(p=m\cdot v=0,01\cdot865=8,65kg.m\)/s
Độ biến thiên động năng:
\(\Delta p=F\cdot\Delta t=0,01\cdot10\cdot10^{-3}=10^{-4}kg.m\)/s

Chọn C.
Chọn hệ trục Ox như hình vẽ
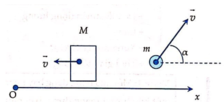
Phương trình bảo toàn véc tơ động lượng cho hệ theo Ox
![]()
Vì trước khi bắn hệ đứng yên
Chiếu phương trình (*) lên Ox ta được: 0 = -p’1 + p’2.cos60o
Thay số ta được:
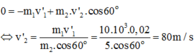

Chọn C.
Chọn hệ trục Ox như hình vẽ
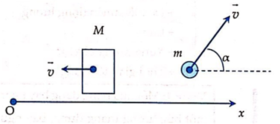
Phương trình bảo toàn véc tơ động lượng cho hệ theo Ox


\(p=mv=0,01.865=8,65\)
\(F=\frac{p}{t}=\frac{8,65}{10^{-3}}=8650N\)
Vậy ................

Giả sử thời gian đạn rời khỏi nòng súng là (rất nhỏ).
Giả sử nội lực của hệ đạn + nòng súng là N.
N làm biến thiên động lượng của đạn (đề đã bỏ qua tác động của trọng trường với đạn).
Hợp lực của N và F ma sát và P làm biến thiên động lượng của nòng.
Chiếu lên phương ngang.
Thay N từ pt trên vào ta tìm được V.

Tham khảo:
m=80(g)=0,08(kg)
v0=0(m/s)
v=1000(m/s)
S=0,6(m)
Động năng của viên đạn khi bay ra khỏi nòng súng là:
Wđ=1/2mv2=1/2.0,08.10002
=40000(J)
Áp dụng định lí độ biến thiên động năng, ta có:
AF=1/2mv2−12mv20
⇔F.S=40000−0=40000
⇔F=40000/S=40000/0,6=2.105/3(N)
Tham khảo:
\(m=80(g)=0,08(g)\)
\(v_0=0 (m/s)\)
\(v=1000(m/s)\)
\(S=0,6(m)\)
Động năng của viên đạn khi bay ra khỏi nòng súng là:
\(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}.0,08.1000^2=40000(J)\)
Áp dụng định lí độ biến thiên động năng, ta có:
\(A_F=\dfrac{1}{2}mv^2-\dfrac{1}{2}mv^2_0\)
`<=>` \(F.S=40000-0=40000\)
`<=>` \(F=\dfrac{40000}{S}=\dfrac{4000}{0,6}=\dfrac{2.10^2}{3}(N)\)

Chọn đáp án B
Hướng dẫn:
Trước khi bắn: p 0 = 0. Do cả sung và đạn đều đứng yên
Sau khi bắn: p = m s ú n g . v s ú n g + m đ ạ n . v đ ạ n
Áp dụng định luật bảo toàn động lượng ta có:
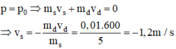
Dấu trừ là để chỉ sung bị giật lùi
Chọn đáp án B