Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định luật bảo toàn động lượng:
\(m_1\overrightarrow{v_1}+m_2\overrightarrow{v_2}=m_1\overrightarrow{v_1'}+m_2\overrightarrow{v_2'}\)
\(\Rightarrow m_1v_1=m_2v_2\)
\(\Leftrightarrow0,01.600=5.v_2\Leftrightarrow v_2=1,2\left(m/s\right)\)

Lúc đầu hệ vật đứng yên có động lượng p 0 = 0. Ngay sau khi bắn, hệ vật có động lượng MV + mv = 0. Áp dụng định luật bảo toàn động lượng cho chuyển động theo phương ngang của hệ vật ta có:
p = p 0 ⇒ MV + mv = 0
suy ra MV = - mv hay V = -mv/M = -10.800/10000 = -0,8(m/s)

Chọn C.
Chọn hệ trục Ox như hình vẽ
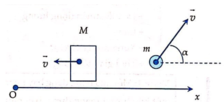
Phương trình bảo toàn véc tơ động lượng cho hệ theo Ox
![]()
Vì trước khi bắn hệ đứng yên
Chiếu phương trình (*) lên Ox ta được: 0 = -p’1 + p’2.cos60o
Thay số ta được:
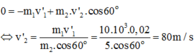

Chọn C.
Chọn hệ trục Ox như hình vẽ
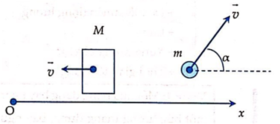
Phương trình bảo toàn véc tơ động lượng cho hệ theo Ox


Theo định luật bảo toàn động lượng ta có:
m . v → + M . V → = 0 → ⇒ V → = − m M v → ⇒ V = − m M = − 3 m / s
Vậy súng giật lùi với vận tốc 3m/s ngược chiều với hướng viên đạn.
Chọn đáp án D

Theo định luật bảo toàn động lượng ta có:
m . v → + M . V → = 0 → ⇒ V → = − m M v →
Vậy súng giật lùi với vận tốc 3m/s ngược chiều với hướng viên đạn.

Bảo toàn động lượng :
\(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{0}\)
\(\Rightarrow M\cdot V+m\cdot v=0\)
\(\Rightarrow8V+40\cdot10^{-3}\cdot600=0\)
\(\Rightarrow V=-3\left(\dfrac{m}{s}\right)\)
Động lường của hệ súng + đạn được bảo toàn
=> \(m_s\overrightarrow{v_s}+m_đ\overrightarrow{v_đ}=0\)
=> vs = \(\dfrac{-m_đv_đ}{m_s}=\dfrac{-0,04.600}{8}=-3\)(m/s) ý A

Chọn đáp án B
Hướng dẫn:
Trước khi bắn: p 0 = 0. Do cả sung và đạn đều đứng yên
Sau khi bắn: p = m s ú n g . v s ú n g + m đ ạ n . v đ ạ n
Áp dụng định luật bảo toàn động lượng ta có:
Dấu trừ là để chỉ sung bị giật lùi