Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vẽ đường thẳng y = 2x -1 trên mặt phẳng tọa độ
Với x = 0 thì y = -1, ta được điểm A(0; -1) thuộc đồ thị hàm số y = 2x – 1
Với x = 1 thì y = 1, ta được điểm B(1; 1) thuộc đường thẳng y = 2x – 1
Đồ thị hàm số y = 2x – 1 là một đường thẳng đi qua hai điểm A(0; -1) và điểm B(1; 1)
b) Vì đường thẳng y = ax + b \(\left( {a \ne 0} \right)\) song song với đường thẳng y = 2x -1 nên a = 2
Đường thẳng dã cho là: y = 2x + b
Vì đường thẳng y = 2x + b đi qua điểm M(1; 3) nên:
3 = 2.1 + b suy ra b = 1
Vậy đường thẳng cần tìm là; y = 2x + 1
* Vẽ đường thẳng y = 2x + 1
Với x = 0 thì y = 1, ta được điểm P(0, 1) thuộc đồ thị hàm số y = 2x + 1
Với x = 1 thì y = 1, ta được điểm Q(1; 3) thuộc đồ thị hàm số y = 2x + 1
Đồ thị hàm số y = 2x + 1 là đường thẳng đi qua hai điểm P(0; 1) và Q(1; 3)

a)
- Ở hình 1a là đồ thị của hàm số \(y = 0,5x + 2\) hệ số \(a = 0,5 > 0\); Dùng thước đo độ kiểm tra ta thấy góc \(\alpha \) là góc nhọn.
- Ở hình 1b là đồ thị của hàm số \(y = - 0,5x + 2\) hệ số \(a = - 0,5 < 0\); Dùng thước đo độ kiểm tra ta thấy góc \(\alpha \) là góc tù.

1:Gọi giao của DO và CB là H
Xét ΔOAD vuông tại A và ΔOBH vuông tại B có
OA=OB
góc AOD=góc BOH
=>ΔOAD=ΔOBH
=>OD=OH
=>ΔCDH cân tại C
=>ΔAOD đồng dạng với ΔBOH
Xét ΔBOH vuông tại B và ΔOCH vuông tại O có
góc BHO chung
=>ΔBOH đồng dang với ΔOCH
=>ΔAOD đồng dạng với ΔOCH
2: ΔCHD cân tại C
=>góc CDH=góc CHD=góc ADH
=>DH là phân giác của góc ADC

b)
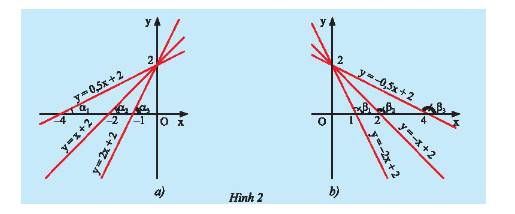
- Ở hình 2a là đồ thị của 3 hàm số \(y = 0,5x + 2;y = x + 2;y = 2x + 2\).
Ta có: \({a_1} = 0,5;{a_2} = 1;{a_3} = 2\) nên \({a_1} < {a_2} < {a_3}\).
Ta có: \({\alpha _1} < {\alpha _2}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
\({\alpha _2} < {\alpha _3}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
Do đó, \({\alpha _1} < {\alpha _2} < {\alpha _3}\).
- Ở hình 2b là đồ thị của 3 hàm số \(y = - 2x + 2;y = - x + 2;y = - 0,5x + 2\).
Ta có: \({a_1} = - 2;{a_2} = - 1;{a_3} = - 0,5\) nên \({a_1} < {a_2} < {a_3}\).
Ta có: \({\beta _1} < {\beta _2}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
\({\beta _2} < {\beta _3}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
Do đó, \({\beta _1} < {\beta _2} < {\beta _3}\).

a: Thay x=1 và y=2 vào y=ax+b, ta được:
\(a\cdot1+b=2\)
=>a+b=2
Thay x=0 và y=1 vào y=ax+b, ta được:
\(a\cdot0+b=1\)
=>b=1
a+b=2
=>a=2-b
=>a=2-1=1
Vậy: phương trình đường thẳng AB là y=x+1
b: Thay x=-1 vào y=x+1, ta được:
\(y=-1+1=0=y_C\)
vậy: C(-1;0) thuộc đường thẳng y=x+1
hay A,B,C thẳng hàng
c: Thay x=3 và y=2 vào y=x+1, ta được:
\(3+1=2\)
=>4=2(sai)
=>D(3;2) không thuộc đường thẳng AB
d: Gọi phương trình đường thẳng (d) cần tìm có dạng là y=ax+b(b\(\ne\)0)
Vì (d) vuông góc với AB nên \(a\cdot1=-1\)
=>a=-1
=>y=-x+b
Thay x=3 và y=2 vào y=-x+b, ta được:
b-3=2
=>b=5
vậy: (d): y=-x+5

a: Gọi hàm số cần tìm có dạng là y=ax+b(a<>0)
Vì đồ thị của hàm số y=ax+b song song với đường thẳng y=5x+1 nên \(\left\{{}\begin{matrix}a=5\\b\ne1\end{matrix}\right.\)
Vậy: y=5x+b
Thay x=2 và y=-3 vào y=5x+b, ta được:
\(b+5\cdot2=-3\)
=>b+10=-3
=>b=-13
Vậy: y=5x-13
b: Thay y=5 vào y=2x-1, ta được:
2x-1=5
=>2x=6
=>x=3
Thay x=3 và y=5 vào y=ax+b, ta được:
\(a\cdot3+b=5\)
=>3a+b=5(1)
Thay x=2 và y=-3 vào y=ax+b, ta được:
2*a+b=-3
=>2a+b=-3(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}3a+b=5\\2a+b=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a+b-2a-b=5-\left(-3\right)\\2a+b=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=8\\b=-3-2a=-3-16=-19\end{matrix}\right.\)
vậy: y=8x-19

Tọa độ giao điểm của hai đường thẳng y=x-7 và y=-4x+3 là:
\(\left\{{}\begin{matrix}x-7=-4x+3\\y=x-7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+4x=7+3\\y=x-7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5x=10\\y=x-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2-7=-5\end{matrix}\right.\)
Thay x=2 và y=-5 vào y=ax+b, ta được:
a*2+b=-5
=>2a+b=-5(1)
thay x=-1 và y=-3 vào y=ax+b, ta được:
a*(-1)+b=-3
=>-a+b=-3(2)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}2a+b=-5\\-a+b=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3a=-2\\a-b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{2}{3}\\b=a-3=-\dfrac{2}{3}-3=-\dfrac{11}{3}\end{matrix}\right.\)
Vậy: (d): \(y=-\dfrac{2}{3}x-\dfrac{11}{3}\)

* Đường thẳng y = ax + b \(\left( {a \ne 0} \right)\)
Vì hệ số góc bằng -1 nên a = -1
Suy ra đường thẳng đã cho là: y = -x + b
Đường thẳng đi qua điểm M(1; 2) nên thay tọa độ điểm M(1; 2) vào đường thẳng y = -x + b ta được:
2 = -x + b suy ra b = 3
Vậy đường thẳng đã cho tìm được là y = -x + 3