Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Để hàm số nghịch biến trên R thì 2m-1<0
=>2m<1
=>\(m< \dfrac{1}{2}\)
b; Thay x=-1 và y=0 vào y=(2m-1)x+m-1, ta được:
\(\left(-1\right)\left(2m-1\right)+m-1=0\)
=>-2m+1+m-1=0
=>-m=0
=>m=0
c: Thay x=1 và y=4 vào y=(2m-1)x+m-1, ta được:
\(1\left(2m-1\right)+m-1=4\)
=>2m-1+m-1=4
=>3m=6
=>m=2
Khi m=2 thì \(y=\left(2\cdot2-1\right)x+2-1=3x+1\)
=>3x-y+1=0
Khoảng cách từ O(0;0) đến đường thẳng 3x-y+1=0 là:
\(d\left(O;\left(d\right)\right)=\dfrac{\left|0\cdot3+0\cdot\left(-1\right)+1\right|}{\sqrt{3^2+\left(-1\right)^2}}=\dfrac{1}{\sqrt{10}}\)

a: Để hàm số y=(2m-1)x+m-1 nghịch biến trên R thì 2m-1<0
=>2m<1
=>\(m< \dfrac{1}{2}\)
b: Thay x=-1 và y=0 vào y=(2m-1)x+m-1, ta được:
-(2m-1)+m-1=0
=>-2m+1+m-1=0
=>-m=0
=>m=0
c: Thay x=1 và y=4 vào y=(2m-1)x+m-1, ta được:
2m-1+m-1=4
=>3m-2=4
=>3m=6
=>m=2
Khi m=2 thì \(y=\left(2\cdot2-1\right)x+2-1=3x+1\)
vẽ đồ thị:
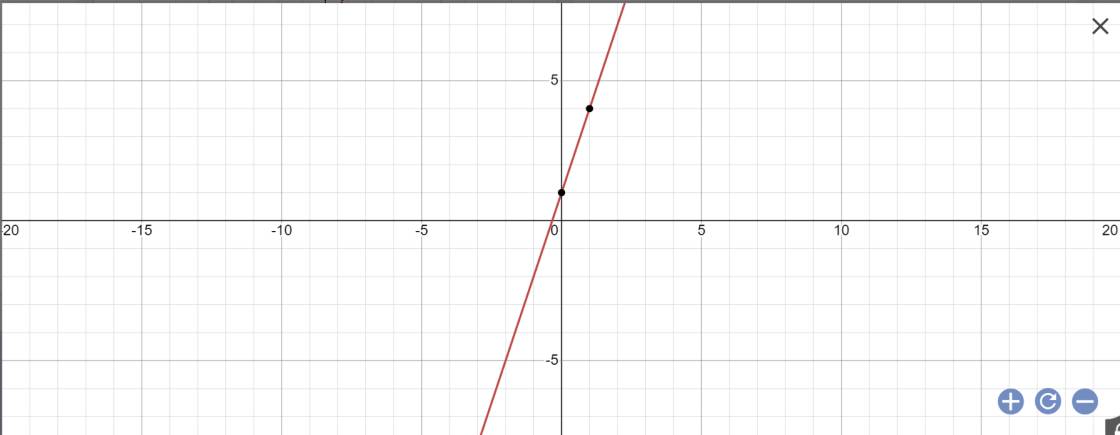
y=3x+1
=>3x-y+1=0
Khoảng cách từ O(0;0) đến đường thẳng 3x-y+1=0 là:
\(d\left(O;3x-y+1=0\right)=\dfrac{\left|0\cdot3+0\cdot\left(-1\right)+1\right|}{\sqrt{3^2+\left(-1\right)^2}}=\dfrac{1}{\sqrt{10}}\)

Vì đồ thị hàm số y=ax+by=ax+b đi qua điểm A(−1;2)A(−1;2) nên ta có:
2=−1.a+b2=−1.a+b suy ra −a+b=2−a+b=2
Vi đồ thị hàm số y=ax+by=ax+b đi qua điểm B(1;4)B(1;4) nên ta có:
4=1.a+b4=1.a+b suy ra a+b=4(2)a+b=4(2)
Từ (1) và (2) ta tìm được a=1;b=3a=1;b=3
Vậy hàm số cần tìm là y=x+3y=x+3.

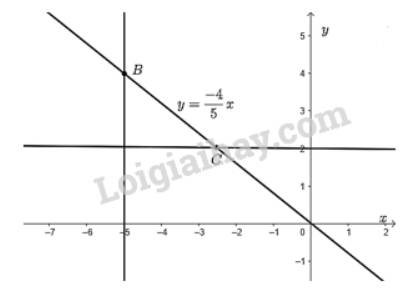
Vẽ đồ thị hàm số \(y = \dfrac{{ - 4}}{5}x\).
Đồ thị hàm số là đường thẳng đi qua hai điểm \(O\) và \(P\).
Từ điểm \(x = - 5\) trên \(Ox\)vẽ đường thẳng vuông góc với \(Ox\) cắt đồ thị hàm số tại điểm \(B\). Khi đó, điểm \(B\) là điểm trên đồ thị hàm số có hoành độ bằng -5.


a: Gọi hàm số cần tìm có dạng là y=ax+b(a<>0)
Vì đồ thị của hàm số y=ax+b song song với đường thẳng y=5x+1 nên \(\left\{{}\begin{matrix}a=5\\b\ne1\end{matrix}\right.\)
Vậy: y=5x+b
Thay x=2 và y=-3 vào y=5x+b, ta được:
\(b+5\cdot2=-3\)
=>b+10=-3
=>b=-13
Vậy: y=5x-13
b: Thay y=5 vào y=2x-1, ta được:
2x-1=5
=>2x=6
=>x=3
Thay x=3 và y=5 vào y=ax+b, ta được:
\(a\cdot3+b=5\)
=>3a+b=5(1)
Thay x=2 và y=-3 vào y=ax+b, ta được:
2*a+b=-3
=>2a+b=-3(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}3a+b=5\\2a+b=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a+b-2a-b=5-\left(-3\right)\\2a+b=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=8\\b=-3-2a=-3-16=-19\end{matrix}\right.\)
vậy: y=8x-19

Từ điểm \(y = 2\) trên \(Oy\) vẽ đường thẳng vuông góc với \(Oy\) cắt đồ thị hàm số tại điểm \(C\). Khi đó, điểm \(C\) là điểm trên đồ thị hàm số có tung độ bằng 2.

a: Thay x=-1 và y=2 vào (d), ta được:
\(-\left(m-2\right)+n=2\)
=>-m+2+n=2
=>-m+n=0
=>m-n=0(1)
Thay x=3 và y=-4 vào (d), ta được:
\(3\left(m-2\right)+n=-4\)
=>3m-6+n=-4
=>3m+n=2(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}m-n=0\\3m+n=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m-n+3m+n=2\\m-n=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4m=2\\n=m\end{matrix}\right.\Leftrightarrow n=m=\dfrac{1}{2}\)
b: Thay x=0 và \(y=1-\sqrt{2}\) vào (d), ta được:
\(0\left(m-2\right)+n=1-\sqrt{2}\)
=>\(n=1-\sqrt{2}\)
Vậy: (d): \(y=\left(m-2\right)x+1-\sqrt{2}\)
Thay \(x=2+\sqrt{2}\) và y=0 vào (d), ta được:
\(\left(m-2\right)\cdot\left(2+\sqrt{2}\right)+1-\sqrt{2}=0\)
=>\(\left(m-2\right)\left(2+\sqrt{2}\right)=\sqrt{2}-1\)
=>\(m-2=\dfrac{\sqrt{2}-1}{2+\sqrt{2}}=\dfrac{-4+3\sqrt{2}}{2}\)
=>\(m=\dfrac{-4+3\sqrt{2}+4}{2}=\dfrac{3\sqrt{2}}{2}\)
c: 2y+x-3=0
=>2y=-x+3
=>\(y=-\dfrac{1}{2}x+\dfrac{3}{2}\)
Để (d) vuông góc với đường thẳng y=-1/2x+3/2 thì
\(-\dfrac{1}{2}\left(m-2\right)=-1\)
=>m-2=2
=>m=4
Vậy: (d): \(y=\left(4-2\right)x+n=2x+n\)
Thay x=1 và y=3 vào y=2x+n, ta được:
\(n+2\cdot1=3\)
=>n+2=3
=>n=1
d: 3x+2y=1
=>\(2y=-3x+1\)
=>\(y=-\dfrac{3}{2}x+\dfrac{1}{2}\)
Để (d) song song với đường thẳng \(y=-\dfrac{3}{2}x+\dfrac{1}{2}\) thì
\(\left\{{}\begin{matrix}m-2=-\dfrac{3}{2}\\n\ne\dfrac{1}{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=\dfrac{1}{2}\\n\ne\dfrac{1}{2}\end{matrix}\right.\)
Vậy: (d): \(y=\left(\dfrac{1}{2}-2\right)x+n=-\dfrac{3}{2}x+n\)
Thay x=1 và y=2 vào (d), ta được:
\(n-\dfrac{3}{2}=2\)
=>\(n=2+\dfrac{3}{2}=\dfrac{7}{2}\left(nhận\right)\)

Do đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng -2,5 nên đi qua điểm (-2,5; 0)
Thay tọa độ điểm (-2,5; 0) vào hàm số, ta có:
2.(-2,5) + b = 0
-5 + b = 0
b = 0 + 5
b = 5
Vậy hàm số cần xác định là: y = 2x + 5

các bạn giải giúp mk với ạ! gia đình xin hậu tạ nhiều!!!!^_^