Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) 4x2 + 4x + 1 = 0 có a = 4, b = 4, b' = 2, c = 1
∆' = 22 – 4 . 1 = 0: Phương trình có nghiệm kép
x1 = x2 = =
b) 13852x2 – 14x + 1 = 0 có a = 13852, b = -14, b’ = -7, c = 1
∆’ = (-7)2 – 13852 . 1 = 49 – 13852 < 0
Phương trình vô nghiệm.
c) 5x2 – 6x + 1 = 0 có a = 5, b = -6, b’ = -3, c = 1
∆’ = (-3)2 – 5 . 1 = 4, √∆’ = 2
x1 = = 1; x2 =
=
d) -3x2 + 4√6x + 4 = 0 có a = -3, b = 4√6, b’ = 2√6, c = 4.
∆’ = (2√6)2 – (-3) . 4 = 24 + 12 = 36, √∆’ = 6
X1 = = ;
, x2 =
=

a) Nếu m = -1 thì : \(4x-3=0\Leftrightarrow x=\frac{3}{4}\) => pt có một nghiệm
Nếu \(m\ne-1\) , xét \(\Delta'=\left(m-1\right)^2-\left(m+1\right)\left(m-2\right)=m^2-2m+1-\left(m^2-m-2\right)=-m+3\)
Để pt có hai nghiệm phân biệt thì \(\Delta>0\) , tức là \(3-m>0\Leftrightarrow m< 3\)
Vậy để pt có hai nghiệm phân biệt thì \(\begin{cases}m< 3\\m\ne-1\end{cases}\)
b) Thay x = 2 vào pt đã cho , tìm được m = -6
Suy ra pt : \(-5x^2+14x-8=0\Leftrightarrow\left(5x-4\right)\left(x-2\right)=0\) \(\Leftrightarrow\left[\begin{array}{nghiempt}x=2\\x=\frac{4}{5}\end{array}\right.\)
Vậy nghiệm còn lại là x = 4/5
c) Áp dụng hệ thức Vi-et , ta có : \(\begin{cases}x_1+x_2=2\left(m-1\right)\\x_1.x_2=m-2\end{cases}\)
\(\frac{1}{x_1}+\frac{1}{x_2}=\frac{7}{4}\Leftrightarrow4\left(x_1+x_2\right)=7x_1.x_2\)
\(\Rightarrow4.\left(2m-2\right)=7.\left(m-2\right)\Leftrightarrow8m-8=7m-14\Leftrightarrow m=-6\)
d) Ta có : \(A=2\left(x_1^2+x_2^2\right)+x_1.x_2=2\left(x_1+x_2\right)^2-3x_1.x_2=8\left(m-1\right)^2-3\left(m-2\right)\)
\(=8m^2-19m+14=8\left(m-\frac{19}{16}\right)^2+\frac{87}{32}\ge\frac{87}{32}\)
=> Min A = 87/32 <=> m = 19/16

a) Dùng hệ thức Viét ta có:
\(x_1x_2=\dfrac{-35}{1}=-35\\ \Leftrightarrow7x_2=-35\\ \Leftrightarrow x_2=-5\\ x_1+x_2=\dfrac{-m}{1}=-m\\ \Leftrightarrow7+\left(-5\right)=-m\\ \Leftrightarrow-m=2\\ \Leftrightarrow m=-2\)
b) Dùng hệ thức Viét ta có:
\(x_1+x_2=\dfrac{-\left(-13\right)}{1}=13\\ \Leftrightarrow12,5+x_2=13\\ \Leftrightarrow x_2=0,5\\ x_1x_2=\dfrac{m}{1}=m\\ \Leftrightarrow12,5\cdot0,5=m\\ \Leftrightarrow m=6,25\)
c) Dùng hệ thức Viét ta có:
\(x_1+x_2=\dfrac{-3}{4}\\ \Leftrightarrow-2+x_2=\dfrac{-3}{4}\\ \Leftrightarrow x_2=\dfrac{5}{4}\\ x_1x_2=\dfrac{-m^2+3m}{4}\\ \Leftrightarrow4x_1x_2=-m^2+3m\\ \Leftrightarrow4\cdot\left(-2\right)\cdot\dfrac{5}{4}+m^2-3m=0\\ \Leftrightarrow m^2-3m-10=0\\ \Leftrightarrow m^2-5m+2m-10=0\\ \Leftrightarrow m\left(m-5\right)+2\left(m-5\right)=0\\ \Leftrightarrow\left(m+2\right)\left(m-5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=-2\\m=5\end{matrix}\right.\)
d) Dùng hệ thức Viét ta có:
\(x_1x_2=\dfrac{5}{3}\\ \Leftrightarrow\dfrac{1}{3}x_2=\dfrac{5}{3}\\ \Leftrightarrow x_2=5\\ x_1+x_2=\dfrac{-\left[-2\left(m-3\right)\right]}{3}=\dfrac{2\left(m-3\right)}{3}=\dfrac{2m-6}{3}\\ \Leftrightarrow3\left(x_1+x_2\right)=2m-6\\ \Leftrightarrow3\left(\dfrac{1}{3}+5\right)=2m-6\\ \Leftrightarrow3\cdot\dfrac{16}{3}+6=2m\\ \Leftrightarrow16+6=2m\\ \Leftrightarrow22=2m\\ \Leftrightarrow m=11\)

Phương trình -3 x 2 + 14x - 8 = 0 có hệ số a = -3, b’= 7, c = -8
Ta có: ∆ ' = b ' 2 – ac = 7 2 – (-3).(-8) = 49 – 24 > 0
∆ ' = 25 = 5
Phương trình có 2 nghiệm phân biệt:
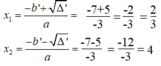

Phương trình 9 x 2 +6x+1 =0 có hệ số a=9,b’=3,c=1
Ta có: ∆ ’ = b ' 2 – ac = 3 2 -9.1 = 9 - 9 = 0
Phương trình có nghiệm kép:
x 1 = x 2 = -b'/a =-3/9 =-1/3

Phương trình 5 x 2 – 6x -1 = 0 có hệ số a = 5, b’ = -3, c = -1
Ta có: ∆ ’ = b ' 2 – ac = - 3 2 -5.(-1) = 9 + 5 = 14 > 0
∆ ' = 14
Phương trình có hai nghiệm phân biệt :
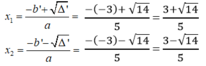


Phương trình -7 x 2 +4x=3 ⇔ 7x2 -4x+3 = 0 có hệ số a=7, b’=-2 , c=3
Ta có: ∆ ’ = b ' 2 – ac = - 2 2 -7.3 = 4- 21= -17 < 0
Vậy phương trình vô nghiệm