K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
AH
Akai Haruma
Giáo viên
7 tháng 7 2021
a. $6x^2-11x=x(6x-11)$
b. $x^7+x^5+1=(x^7-x)+(x^5-x^2)+x+x^2+1$
$=x(x^6-1)+x^2(x^3-1)+(x^2+x+1)$
$=x(x^3-1)(x^3+1)+x^2(x^3-1)+(x^2+x+1)$
$=(x^3-1)(x^4+x+x^2)+(x^2+x+1)$
$=(x-1)(x^2+x+1)(x^4+x^2+x)+(x^2+x+1)$
$=(x^2+x+1)[(x-1)(x^4+x^2+x)+1]$
$=(x^2+x+1)(x^5-x^4+x^3-x+1)$
AH
Akai Haruma
Giáo viên
7 tháng 7 2021
c.
$x^8+x^4+1=(x^4)^2+2.x^4+1-x^4$
$=(x^4+1)^2-(x^2)^2$
$=(x^4+1-x^2)(x^4+1+x^2)$
$=(x^4+1-x^2)(x^4+2x^2+1-x^2)$
$=(x^4-x^2+1)[(x^2+1)^2-x^2]$
$=(x^4-x^2+1)(x^2+1-x)(x^2+1+x)$
d.
$x^3-5x+8-4=x^3-5x+4$
$=x^3-x^2+x^2-x-(4x-4)$
$=x^2(x-1)+x(x-1)-4(x-1)=(x-1)(x^2+x-4)$
e.
$x^5+x^4+1=(x^5-x^2)+(x^4-x)+x^2+x+1$
$=x^2(x^3-1)+x(x^3-1)+x^2+x+1$
$=(x^3-1)(x^2+x)+(x^2+x+1)$
$=(x-1)(x^2+x+1)(x^2+x)+(x^2+x+1)$
$=(x^2+x+1)[(x-1)(x^2+x)+1]$
$=(x^2+x+1)(x^3-x+1)$
T
26 tháng 8 2023
\(x^5+x^4+x+1=0\)
\(\Leftrightarrow x^4\left(x+1\right)+\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^4+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x^4+1=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^4=-1\end{matrix}\right.\)
\(\Rightarrow x=-1\) (do \(x^4\ge0\forall x\))
Vậy x = -1
H9
HT.Phong (9A5)
CTVHS
26 tháng 8 2023
\(x^5+x^4+x+1=0\)
\(\Leftrightarrow\left(x^5+x^4\right)+\left(x+1\right)=0\)
\(\Leftrightarrow x^4\left(x+1\right)+\left(x+1\right)=0\)
\(\Leftrightarrow\left(x^4+1\right)\left(x+1\right)=0\) (Mà: \(x^4+1\ge1>0\forall x\))
\(\Leftrightarrow x+1=0\)
\(\Leftrightarrow x=-1\)
26 tháng 8 2021
a: \(x^4+4=\left(x^2-2x+2\right)\left(x^2+2x+2\right)\)
b: \(x^8+x^7+1\)
\(=x^8+x^7+x^6-x^6-x^5-x^4+x^5+x^4+x^3-x^3-x^2-x+x^2+x+1\)
\(=\left(x^2+x+1\right)\left(x^6-x^4+x^3-x+1\right)\)
c: \(x^8+x^4+1\)
\(=\left(x^8+2x^4+1\right)-x^4\)
\(=\left(x^4-x^2+1\right)\cdot\left(x^4+x^2+1\right)\)
\(=\left(x^4-x^2+1\right)\left(x^2+1-x\right)\left(x^2+1+x\right)\)
23 tháng 12 2017
M là số lớn nhất trong các số x1+x2x2+x3,x3+x4,x4+x5,
suy ra;3M >=(x1+x2)+(x2+x3)+(x4+x5)
suy ra 3M >=300+X2
suy ra M>=100+X2/3>=100
Với x2=x4=0,x1=x3=x5=100 thì M =100
Vậy GTNN của M =100
CM
18 tháng 1 2017
xS = x.( 1 + x + x 2 + x 3 + x 4 + x 5 ) = x + x 2 + x 3 + x 4 + x 5 + x 6
=> xS – S = x + x 2 + x 3 + x 4 + x 5 + x 6 - 1 - x - x 2 - x 3 - x 4 - x 5 = x 6 – 1
Đáp án cần chọn là: A
5 tháng 4 2020
Vì P(x) có hệ số bậc cao nhất là 1
Nên P(x) có thể được viết dưới dạng: \(P\left(x\right)=\left(x-x_1\right)\left(x-x_2\right)\left(x-x_3\right)\left(x-x_4\right)\left(x-x_5\right)\)
Và \(P\left(-1\right)=\left(-1\right)^5-5\left(-1\right)^3+4\left(-1\right)+1=1\)
\(P\left(\frac{1}{2}\right)=\frac{77}{32}\)
Ta có: \(Q\left(x\right)=2x^2+x-1=2x^2+2x-x-1=2x\left(x+1\right)-\left(x+1\right)=\left(x+1\right)\left(2x-1\right)\)
=> \(Q\left(x_1\right).\text{}\text{}Q\left(x_2\right).\text{}\text{}Q\left(x_3\right).\text{}\text{}Q\left(x_4\right).\text{}\text{}Q\left(x_5\right)\text{}\text{}\)
\(=\left(x_1+1\right)\left(2x_1-1\right)\left(x_2+1\right)\left(2x_2-1\right)\left(x_3+1\right)\left(2x_3-1\right)\left(x_4+1\right)\left(2x_4-1\right)\left(x_5+1\right)\left(2x_5-1\right)\)
\(=32\left(-1-x_1\right)\left(\frac{1}{2}-x_1\right)\left(-1-x_2\right)\left(\frac{1}{2}-x_2\right)\left(-1-x_3\right)\left(\frac{1}{2}-x_3\right)\left(-1-x_4\right)\left(\frac{1}{2}-x_4\right)\left(-1-x_5\right)\left(\frac{1}{2}-x_5\right)\)\(=32.P\left(-1\right).P\left(\frac{1}{2}\right)=32.1.\frac{77}{32}=77\)
7 tháng 4 2020
\(p\left(x\right)=x^5-5x^3+4x+1=\left(x-x_1\right)\left(x-x_2\right)\left(x-x_3\right)\left(x-x_4\right)\left(x-x_5\right)\)
\(Q\left(x\right)=2\left(\frac{1}{2}-x\right)\left(-1-x\right)\)
Do đó \(Q\left(x_1\right)\cdot Q\left(x_2\right)\cdot Q\left(x_3\right)\cdot Q\left(x_4\right)\cdot Q\left(x_5\right)\)
\(=2^5\left[\left(\frac{1}{2}-x_1\right)\left(\frac{1}{2}-x_2\right)\left(\frac{1}{2}-x_3\right)\left(\frac{1}{2}-x_4\right)\left(\frac{1}{2}-x_5\right)\right]\)
\(=\left(-1-x_1\right)\left(-1-x_2\right)\left(-1-x_3\right)\left(-1-x_4\right)\left(-1-x_5\right)\)
\(=32P\left(\frac{1}{2}\right)\cdot\left[P\left(-1\right)\right]\)
\(=32\cdot\left(\frac{1}{32}-\frac{5}{8}+\frac{4}{2}+1\right)\left(-1+5-4+1\right)\)
\(=4300\)
*Mình không chắc*
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 3 2020
1.
a/ \(\Leftrightarrow\left(x+1\right)\left(x^2+3x+2\right)+\left(x-1\right)\left(x^2-3x+2\right)-12=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2\right)+3x\left(x+1\right)-3x\left(x-1\right)+\left(x-1\right)\left(x^2+2\right)-12=0\)
\(\Leftrightarrow2x\left(x^2+2\right)+6x^2-12=0\)
\(\Leftrightarrow x^3+3x^2+2x-6=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+4x+6\right)=0\Rightarrow x=1\)
b/ Nhận thấy \(x=0\) ko phải nghiệm, chia 2 vế cho \(x^2\)
\(x^2+\frac{1}{x^2}+3\left(x+\frac{1}{x}\right)+4=0\)
Đặt \(x+\frac{1}{x}=t\Rightarrow x^2+\frac{1}{x^2}=t^2-2\)
\(t^2-2+3t+4=0\Rightarrow t^2+3t+2=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=-2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x+\frac{1}{x}=-1\\x+\frac{1}{x}=-2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x^2+x+1=0\left(vn\right)\\x^2+2x+1=0\end{matrix}\right.\) \(\Rightarrow x=-1\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 3 2020
1c/
\(\Leftrightarrow x^5+x^4-2x^4-2x^3+5x^3+5x^2-2x^2-2x+x+1=0\)
\(\Leftrightarrow x^4\left(x+1\right)-2x^3\left(x+1\right)+5x^2\left(x+1\right)-2x\left(x+1\right)+x+1=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^4-2x^3+5x^2-2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^4-2x^3+5x^2-2x+1=0\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow x^4-2x^3+x^2+x^2-2x+1+3x^2=0\)
\(\Leftrightarrow\left(x^2-x\right)^2+\left(x-1\right)^2+3x^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-x=0\\x-1=0\\x=0\end{matrix}\right.\) \(\Rightarrow\) không tồn tại x thỏa mãn
Vậy pt có nghiệm duy nhất \(x=-1\)
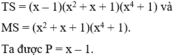
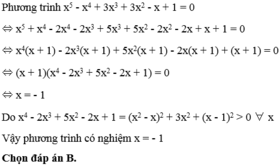
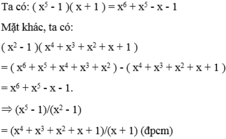
= x5-x4+x3-x3-1=x2(x2-x+1) -(x+1)(x^2 -x+1)=(x2-x-1)(x2-x-1)
= x5 -x4+x3-x3-1=x3(x2-x+1)-(x+1)(x^2-x+1)=(x2-x+1)(x3-x-1)