
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


TXĐ: D=\(\left[-2;2\right]\)
Đặt \(\sqrt{x+2}+\sqrt{2-x}=a\ge0\Rightarrow a^2=4+2\sqrt{-x^2+4}\)
Khi đó: pt trở thành: \(a+a^2+2m-1=0\) (*)
để pt đã cho có nghiệm thì pt(*) có nghiệm
khi đó \(\Delta=1^2-4\left(2m-1\right)=-8m+2\ge0\Rightarrow m\le\dfrac{1}{4}\)
???

Đặt t = x + 2 + 2 − x
Điều kiện t = x + 2 + 2 − x ≥ x + 2 + 2 − x = 2 ⇒ t ≥ 2
Lại có x + 2 + 2 − x ≤ 1 2 + 1 2 . x + 2 + 2 − x = 2 2 ⇒ t ≤ 2 2
Suy ra 2 ≤ t ≤ 2 2
Ta có: t 2 = 4 + 2 4 − x 2 ⇒ 2 4 − x 2 = t 2 − 4
Phương trình trở thành: t + t 2 − 4 − 2 m + 3 = 0 ⇔ t 2 + t − 2 m − 1 = 0
⇔ t 2 + t − 1 = 2 m *
Xét hàm số f ( x ) = t 2 + t − 1 (parabol có hoành độ đỉnh x = − 1 2 ∉ 2 ; 2 2 ) trên 2 ; 2 2 , có bảng biến thiên
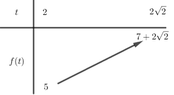
Phương trình (∗) có nghiệm thỏa 2 ≤ t ≤ 2 2 khi 5 ≤ 2 m ≤ 7 + 2 2
⇒ 5 2 ≤ m ≤ 7 + 2 2 2
5 2 ≤ m ≤ 7 + 2 2 2 → 2 , 5 ≤ m ≤ 4 , 91
Vậy có 2 giá trị m nguyên dương là m = 3 , m = 4
Đáp án cần chọn là: D

ĐKXĐ: \(-2\le x\le2\)
Đặt \(\sqrt{x+2}+\sqrt{2-x}=t\Rightarrow\left\{{}\begin{matrix}2\le t\le2\sqrt{2}\\2\sqrt{-x^2+4}=t^2-4\end{matrix}\right.\)
Pt trở thành:
\(t+t^2-4+2m+3=0\)
\(\Leftrightarrow t^2+t-1=-2m\)
Xét hàm \(f\left(t\right)=t^2+t-1\) trên \(\left[2;2\sqrt{2}\right]\)
\(-\dfrac{b}{2a}=-\dfrac{1}{2}\notin\left[2;2\sqrt{2}\right]\)
\(f\left(2\right)=5\) ; \(f\left(2\sqrt{2}\right)=7+2\sqrt{2}\)
\(\Rightarrow5\le-2m\le7+2\sqrt[]{2}\)
\(\Rightarrow-\dfrac{7+2\sqrt{2}}{2}\le m\le-\dfrac{5}{2}\)
Có đúng 1 giá trị nguyên của m thỏa mãn là \(m=-4\)

ĐK: \(-2\le x\le2\)
Đặt \(\sqrt{x+2}+\sqrt{2-x}=t\left(2\le t\le2\sqrt{2}\right)\)
Phương trình đã cho trở thành:
\(t+t^2-4+2m+3=0\)
\(\Leftrightarrow2m=f\left(t\right)=-t^2-t+1\)
Phương trình đã cho có nghiệm khi \(minf\left(t\right)\le2m\le maxf\left(t\right)\)
\(\Leftrightarrow-7-2\sqrt{2}\le2m\le-5\)
\(\Leftrightarrow\dfrac{-7-2\sqrt{2}}{2}\le m\le-\dfrac{5}{2}\)
Có bao nhiêu giá trị nguyên của tham số m để phương trình x^2 -2|x| +1-m = 0 có 4 nghiệm phân biệt ?


Pt đã cho có 2 nghiệm pb khi:
\(\left\{{}\begin{matrix}m+1\ne0\\\Delta'=\left(m+3\right)^2-\left(m+1\right)\left(2m+9\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-1\\-m^2-5m>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-1\\-5< m< 0\end{matrix}\right.\)
\(\Rightarrow m=\left\{-4;-3;-2\right\}\) có 3 giá trị nguyên
chỉ có 1 nghiệm là 0