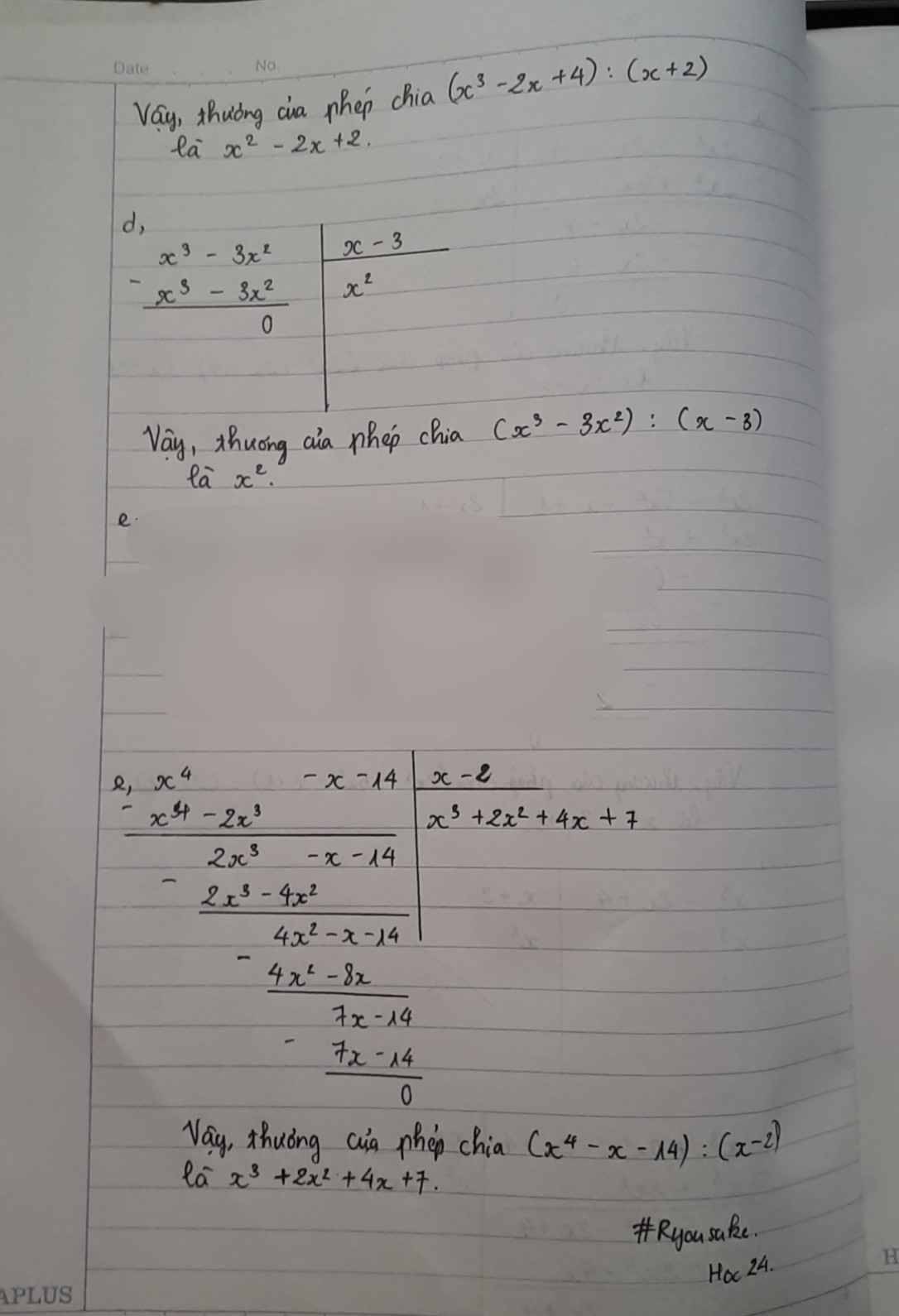VV
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 1 2021
a, \(3x+2\left(x-5\right)=6-\left(5x-1\right)\)
\(\Leftrightarrow3x+2x-10=6-5x+1\)
\(\Leftrightarrow-15\ne0\)Vậy phương trình vô nghiệm
b, \(x^3-3x^2-x+3=0\)
\(\Leftrightarrow x\left(x^2-1\right)-3\left(x^2-1\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-1\right)\left(x+1\right)=0\Leftrightarrow x=3;\pm1\)
Vậy tập nghiệm của phương trình là S = { 1 ; -1 ; 3 }
27 tháng 1 2021
c, \(\frac{1}{x-3}+\frac{x}{x+3}=\frac{2}{x^2-9}ĐK:x\ne\pm3\)
\(\Leftrightarrow\frac{x+3}{\left(x-3\right)\left(x+3\right)}+\frac{x\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}=\frac{2}{\left(x-3\right)\left(x+3\right)}\)
\(\Leftrightarrow x+3+x^2-3x-2=0\)
\(\Leftrightarrow x^2-2x+1=0\Leftrightarrow\left(x-1\right)^2=0\Leftrightarrow x=1\)thỏa mãn
Vậy ...
18 tháng 6 2019
\(a,\left(3x-5\right)\left(7-5x\right)-\left(5x+2\right)\left(2-3x\right)=4\)
\(\Leftrightarrow21x-15x^2-35+25x-10x+15x^2-4+6x=4\)
\(\Leftrightarrow42x-43=0\)
\(\Leftrightarrow x=\frac{43}{42}\)
\(b,\left(x+2\right)\left(x^2-2x+4\right)-\left(x^3+3\right)x=14\)
\(\Leftrightarrow x^3+8-x^4-3x=14\)
\(\Leftrightarrow-x^4+x^3-3x-6=0\)( vô nghiệm)
Vậy \(x\in\varnothing\)
M
18 tháng 6 2019
a, \((3x-5).(7-5x)-(5x+2).(2-3x)=4\)
\(21x-15x^2-35+25x-[10x-15x^2+4-6x]=4\)
\(21x-15x^2-35+25x-10x+15x^2-4+6x=4\)
\(42x-39=4\)
\(42x=43\)
=> \(x=43/42\)
b, \((x+2).(x^2-2x+4)-(x^3+3).x = 14\)
\(x^3-2x^2+4x+2x^2-4x+8-[x^4+3x]=14\)
\(x^3-2x^2+4x+2x^2-4x+8-x^4-3x=14\)
\(x^3+8-x^4-3x =14 \)
\(-x^4+x^3-3x+8=14\)
\(-x^4+x^3-3x-6=0 ( vô nghiệm ) \)
=> x ∈ ∅
13 tháng 6 2023
a: \(=\dfrac{2\left(x+2\right)\left(x-1\right)}{x+2}=2x-2\)
b: \(=\dfrac{2x^3+x^2-6x^2-3x+2x+1}{2x+1}=x^2-3x+1\)
c: \(=\dfrac{x^3+2x^2-2x^2-4x+2x+4}{x+2}=x^2-2x+2\)
d: \(=\dfrac{x^2\left(x-3\right)}{x-3}=x^2\)
