K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2 tháng 4 2023
a: =(x^2+3x)(x^2+3x+2)+1
=(x^2+3x)^2+2(x^2+3x)+1
=(x^2+3x+1)^2>=0 với mọi x
b: (a^2+b^2+c^2)(x^2+y^2+z^2)-(ax+by+cz)^2
=a^2x^2+a^2y^2+a^2z^2+b^2x^2+b^2y^2+b^2z^2+c^2x^2+c^2y^2+c^2z^2-a^2x^2-b^2y^2-c^2z^2-2axby-2axcz-2bycz
=(a^2y^2-2axby+b^2x^2)+(a^2z^2-2azcx+c^2x^2)+(b^2z^2-2bzcy+c^2y^2)
=(ay-bx)^2+(az-cx)^2+(bz-cy)^2>=0(luôn đúng)
L
2
2 tháng 10 2021
\(-25x^2+5x-1=-\left(25x^2-5x+\dfrac{1}{4}\right)-\dfrac{3}{4}=-\left(5x-\dfrac{1}{2}\right)^2-\dfrac{3}{4}\le-\dfrac{3}{4}< 0\forall x\)
tại x = 18; y = 4
9 tháng 9 2021
\(1,x^2-x+1=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}>0\\ 2,-2x^2-x-1=-2\left(x^2+2\cdot\dfrac{1}{4}x+\dfrac{1}{16}+\dfrac{7}{16}\right)\\ =-2\left(x+\dfrac{1}{4}\right)^2-\dfrac{7}{8}\le-\dfrac{7}{8}< 0\\ 3,\dfrac{1}{2}x^2-2x+2=\dfrac{1}{2}\left(x^2-4x+4\right)=\dfrac{1}{2}\left(x-2\right)^2\ge0\)
29 tháng 11 2016
\(x^2-x+1=x^2-2.\frac{1}{2}x+\frac{1}{2^2}+\frac{3}{4}.\)
\(\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}>0\)
pp bien doi ve tong binh phuong
CM
16 tháng 8 2017
Ta có:
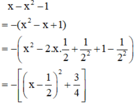
Ta có: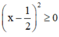 
với mọi số thực x
⇒ 
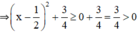với mọi số thực x
⇒ 
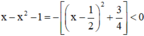với mọi số thực (ĐPCM)
PT
1
CM
17 tháng 11 2017
Ta có:
x2 – 2xy + y2 + 1
= (x2 – 2xy + y2) + 1
= (x – y)2 + 1.
(x – y)2 ≥ 0 với mọi x, y ∈ R
⇒ x2 – 2xy + y2 + 1 = (x – y)2 + 1 ≥ 0 + 1 = 1 > 0 với mọi x, y ∈ R (ĐPCM).
PT
1
CM
20 tháng 4 2019
P = x2 - 2x + 2 = (x – 1)2 + 1
Do (x – 1)2 ≥ 0 ∀x nên (x – 1)2 + 1 ≥ 1 ∀x
Vậy P luôn lớn hơn 0 với mọi x.