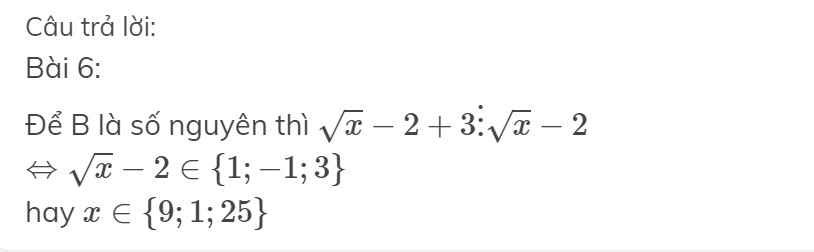K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NC
1
DD
Đoàn Đức Hà
Giáo viên
10 tháng 2 2022
\(\left(\frac{1}{13}x-7\right)^8+\left(\frac{1}{17}y-7\right)^6=0\)
\(\Leftrightarrow\hept{\begin{cases}\frac{1}{13}x-7=0\\\frac{1}{17}y-6=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=91\\y=102\end{cases}}\)
\(x+y=91+102=193\)
17 tháng 7 2022
Bài 6:
Để B là số nguyên thì \(\sqrt{x}-2+3⋮\sqrt{x}-2\)
\(\Leftrightarrow\sqrt{x}-2\in\left\{1;-1;3\right\}\)
hay \(x\in\left\{9;1;25\right\}\)
TM
11 tháng 3 2017
Vì \(\left(\frac{1}{13}x-7\right)^8\ge0;\left(\frac{1}{17}y-7\right)^6\ge0\)=>\(\left(\frac{1}{13}x-7\right)^8+\left(\frac{1}{17}y-7\right)^6\ge0\)
Dấu "=" xảy ra khi \(\left(\frac{1}{13}x-7\right)^8=\left(\frac{1}{17}y-7\right)^6=0\Leftrightarrow\frac{1}{13}x-7=\frac{1}{17}y-7=0\)
<=>\(\frac{1}{13}x=\frac{1}{17}y=7\Leftrightarrow x=\frac{7}{\frac{1}{13}}=91;y=\frac{7}{\frac{1}{17}}=119\Rightarrow x+y=91+119=210\)
Vậy .................
8 tháng 4 2020
a) Với x = 11 <=> 12 = x+1
\(A\left(x\right)=x^{17}-\left(x+1\right)x^{16}+\left(x+1\right)x^{15}-...+12x-1\)
\(A\left(x\right)=12x-11=12.11-1=120\)
b) \(B=6x-6y+10-3ax+3ay+15a\)
\(B=6\left(x-y\right)+10-3a\left(x-y\right)+15a\)
\(B=6.5+10-3.a.5+15a\)
\(B=40\)
c)\(C=\frac{x-y}{x+6}=\frac{x-y}{x+x-2y}=\frac{x-y}{2\left(x-y\right)}=\frac{1}{2}\left(x-2y=6\right)\)
\(C=\frac{2x+6}{3x-2y}+\frac{2y-6}{4y-x}\)
\(C=\frac{2x+1-2y}{3x-2y}+\frac{2y-x+2y}{4y-x}\)
\(C=1+1=2\)
d) ta có : x-y-x = 0
\(\Rightarrow\left\{{}\begin{matrix}x-z=y\\x-y=z\\x=y+z\end{matrix}\right.\).Thay vào B, ta có :
\(B=\frac{x-z}{x}.\frac{y-x}{y}.\frac{z+y}{z}\)
\(B=\frac{y}{x}.\frac{\left(-z\right)}{y}.\frac{x}{z}\)
B= -1