
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{6}{\sqrt{x}-1}-\dfrac{2\sqrt{3}}{\sqrt{x}-1}\)
\(=\dfrac{\sqrt{x}-6-2\sqrt{3}}{\sqrt{x}-1}\)
b: \(=\dfrac{3-\sqrt{x}-1+\sqrt{x}+5\sqrt{x}}{\sqrt{x}-2}=\dfrac{5\sqrt{x}+2}{\sqrt{x}-2}\)
c: \(=\dfrac{2-6\sqrt{x}-1+\sqrt{x}-3+\sqrt{x}}{\sqrt{x}-4}\)
\(=\dfrac{-4\sqrt{x}-4}{x-4}\)

mầy câu 1;3;;4;5 cách làm nhu nhau(nhân liên hop hoac bình phuong lên)
1.
\(DK:x\in\left[-4;5\right]\)
\(\Leftrightarrow\sqrt{x-5}+\left(\sqrt{x+4}-3\right)=0\)
\(\Leftrightarrow\sqrt{x-5}+\frac{x-5}{\sqrt{x+4}+3}=0\)
\(\Leftrightarrow\sqrt{x-5}\left(1+\frac{\sqrt{x-5}}{\sqrt{x+4}+3}\right)=0\)
Vi \(1+\frac{\sqrt{x-5}}{\sqrt{x+4}+3}>0\)
\(\Rightarrow\sqrt{x-5}=0\)
\(x=5\left(n\right)\)
Vay nghiem cua PT la \(x=5\)
2.
\(DK:x\ge0\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x}-2\right)^2}+\sqrt{\left(\sqrt{x}-3\right)^2}=1\)
\(\Leftrightarrow|\sqrt{x}-2|+|\sqrt{x}-3|=1\)
Ta co:
\(|\sqrt{x}-2|+|\sqrt{x}-3|=|\sqrt{x}-2|+|3-\sqrt{x}|\ge|\sqrt{x}-2+3-\sqrt{x}|=1\)
Dau '=' xay ra khi \(\left(\sqrt{x}-2\right)\left(3-\sqrt{x}\right)\ge0\)
TH1:
\(\hept{\begin{cases}\sqrt{x}-2\ge0\\3-\sqrt{x}\ge0\end{cases}\Leftrightarrow4\le x\le9\left(n\right)}\)
TH2:(loai)
Vay nghiem cua PT la \(x\in\left[4;9\right]\)

1)
<=> \(x^2-3x=0\)
\(\Leftrightarrow x\left(x-3\right)=0\)
x= 0
x = 3
2) <=> \(x\left(x-3\right)=4\)
=> \(x=\dfrac{4}{x}+3\)
\(2,x^2-3x=4\)
\(\Leftrightarrow x^2-3x-4=0\)
\(\Delta=b^2-4ac=\left(-3\right)^2-4\left(-4\right)=25>0\)
\(\Rightarrow\)Pt có 2 nghiệm pb
\(\left\{{}\begin{matrix}x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{3+5}{2}=4\\x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-3-5}{2}=-1\end{matrix}\right.\)
Vậy \(S=\left\{4;-1\right\}\)
\(3,x^4-5x^2+6=0\)
Đặt \(t=x^2\left(t\ge0\right)\)
Pt trở thành
\(t^2-5t+6=0\)
\(\Delta=b^2-4ac=\left(-5\right)^2-4.6=1>0\)
\(\Rightarrow\)Pt ó 2 nghiệm pb
\(\left\{{}\begin{matrix}x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{5+1}{2}=3\\x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-5-1}{2}-3\end{matrix}\right.\)
\(\Rightarrow t=x^2\Leftrightarrow t=\pm\sqrt{3}\)
Vậy \(S=\left\{\pm\sqrt{3}\right\}\)

a) ĐK: \(x\ge1\)
\(\sqrt{x+1}=x-1\)
\(\Rightarrow x+1=x^2-2x+1\)
\(\Rightarrow3x=x^2\) (1)
Do \(x\ne0\) nên chia mỗi vế của (1) cho x, ta được x = 3 (t/m)

a/ \(\left(x+3\right)\left(3\left(x^2+1\right)^2+2\left(x+3\right)^2\right)=5\left(x^2+1\right)^3\)
\(\Leftrightarrow3\left(x+3\right)\left(x^2+1\right)^2+2\left(x+3\right)^3-5\left(x^2+1\right)^3=0\)
\(\Leftrightarrow3\left(x+3\right)\left(x^2+1\right)^2-3\left(x^2+1\right)^3+2\left(x+3\right)^3-2\left(x^2+1\right)^3=0\)
\(\Leftrightarrow3\left(x^2+1\right)^2\left(-x^2+x+2\right)+2\left(-x^2+x+2\right)\left(\left(x+3\right)^2+\left(x+3\right)\left(x^2+1\right)+\left(x^2+1\right)^2\right)=0\)
\(\Leftrightarrow\left(-x^2+x+2\right)\left[3\left(x^2+1\right)^2+2\left(x+3+\dfrac{x^2+1}{2}\right)^2+\dfrac{3\left(x^2+1\right)^2}{4}\right]=0\)
\(\Leftrightarrow-x^2+x+2=0\) (phần ngoặc phía sau luôn dương)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
b/ \(3\left(x^2+2x-1\right)^2-2\left(x^2+3x-1\right)^2+5\left(x^2+3x-1-\left(x^2+2x-1\right)\right)^2=0\)
Đặt \(\left\{{}\begin{matrix}a=x^2+2x-1\\b=x^2+3x-1\end{matrix}\right.\)
\(3a^2-2b^2+5\left(b-a\right)^2=0\Leftrightarrow8a^2+3b^2-10ab=0\)
\(\Leftrightarrow\left(4a-3b\right)\left(2a-b\right)=0\Leftrightarrow\left[{}\begin{matrix}4a=3b\\2a=b\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4\left(x^2+2x-1\right)=3\left(x^2+3x-1\right)\\2\left(x^2+2x-1\right)=x^2+3x-1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x^2-x-1=0\\x^2+x-1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1+\sqrt{5}}{2}\\x=\dfrac{1-\sqrt{5}}{2}\\x=\dfrac{-1+\sqrt{5}}{2}\\x=\dfrac{-1-\sqrt{5}}{2}\end{matrix}\right.\)
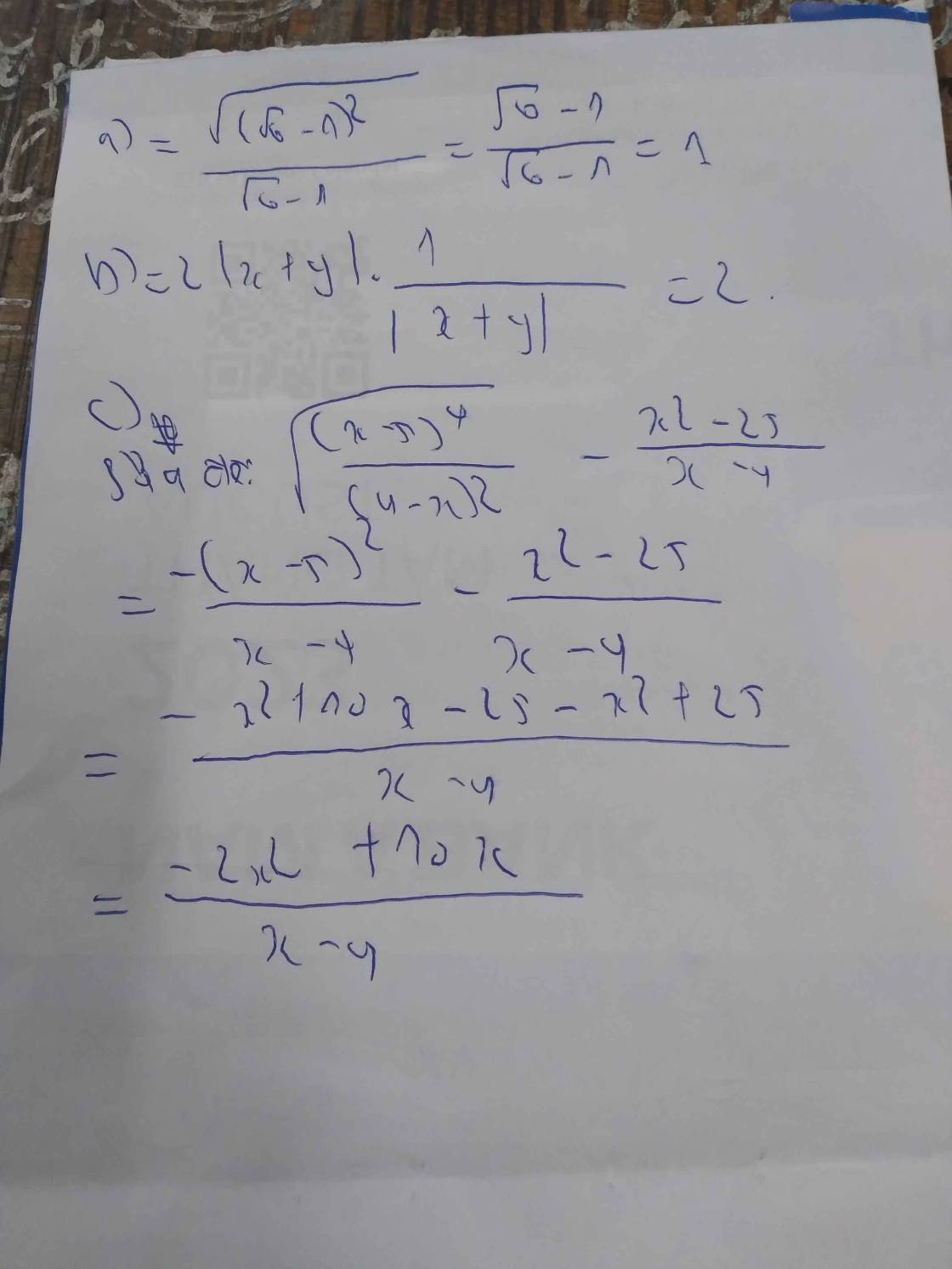
đk: \(2\le x\le4\)
gợi ý đặt 3-x=a; x+2=b
pt đã cho (=) \(\sqrt{b-4}-\sqrt{a+1}=ab\)(đk của a,b nhé)
lại có a+b=5
bạn thế vào nhé nó sẽ lên pt bậc 4 như sau: a4-10a3+33a2-20a=0
Ta có :
\(\sqrt{x-2}-\sqrt{4-x}=x-x^2+6\)
\(ĐKXĐ:2\le x\le4\)
\(PT\Leftrightarrow\frac{x-2-\left(4-x\right)}{\sqrt{x-2}+\sqrt{4-x}}=-x^2+x+6\)
\(\Leftrightarrow\frac{2x-6}{\sqrt{x-2}+\sqrt{4-x}}=\left(3-x\right)\left(x+2\right)\)
\(\Leftrightarrow\left(x-3\right)\left(\frac{2}{\sqrt{x-2}+\sqrt{4-x}}+x+2\right)=0\)
\(\Rightarrow x=3\) ( do \(\frac{2}{\sqrt{x-2}+\sqrt{4-x}}+x+2>0\forall2\le x\le4\) )
Vậy \(x=3\)