K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
12 tháng 10 2017
Bài 1
1.(x-3)(x+2)-x(x-7)=15
\(\Leftrightarrow x^2+2x-3x-6-x^2+7x=15\)
\(\Leftrightarrow-6+6x=15\)
\(\Leftrightarrow6x=15+6\) =21
\(\Rightarrow x=\dfrac{21}{6}=3,5\)
2.(x-5)(x+5)+x(3-x)=20
\(\Leftrightarrow x^2-25+3x-x^2=20\)
\(\Leftrightarrow-25+3x=20\)
\(\Leftrightarrow3x=20+25=45\)
\(\Rightarrow x=\dfrac{45}{3}=15\)
3.(x-7)2-x(2+x)=-7
\(\Leftrightarrow x^2-14x+49-2x-x^2=-7\)
\(\Leftrightarrow-16x+49=-7\)
\(\Leftrightarrow-16x=-7-49=-56\)
\(\Rightarrow x=\dfrac{-56}{-16}=\dfrac{7}{2}=3,5\)
12 tháng 10 2017
Tiếp bài 1
4.(x-4)2-(x+4)(x-4)=-16
\(\Leftrightarrow x^2-8x+16-x^2-16=-16\)
\(\Leftrightarrow-8x=-16\)
\(\Rightarrow x=\dfrac{-16}{-8}=2\)
5.(x-5)(x+5)-x(2-3x)=4x2-7
\(\Leftrightarrow x^2-25-2x+3x^2=4x^2-7\)
\(\Leftrightarrow4x^2-25-2x+3x^2=4x^2-7\)
\(\Leftrightarrow4x^2-4x^2-2x=-7+25\)
\(\Leftrightarrow-2x=18\)
\(\Rightarrow x=\dfrac{18}{-2}=-9\)
5 tháng 12 2017
b) \(x^5+x+1=x^5-x^2+x^2+x+1=x^2\left(x^3-1\right)+x^2+x+1=x^2\left(x-1\right)\left(x^2+x+1\right)+x^2+x+1=\left(x^2+x+1\right)\left[x^2\left(x-1\right)+1\right]\)
3 tháng 7 2022
a: \(\dfrac{1}{x-2}+3=\dfrac{3-x}{x-2}\)
=>1+3x-6=3-x
=>3x-5=3-x
=>4x=8
hay x=2(loại)
b: \(\Leftrightarrow8-x-8\left(x-7\right)=-26\)
=>8-x-8x+56=-26
=>-9x+64=-26
=>-9x=-90
hay x=10(nhận)
c: \(\dfrac{1}{x-2}+\dfrac{1}{x-3}=\dfrac{2}{x-1}\)
\(\Leftrightarrow\dfrac{x-3+x-2}{\left(x-2\right)\left(x-3\right)}=\dfrac{2}{x-1}\)
\(\Leftrightarrow\left(x-1\right)\left(2x-5\right)=2\left(x^2-5x+6\right)\)
\(\Leftrightarrow2x^2-5x-2x+5=2x^2-10x+12\)
=>-7x+10x=12-5
=>3x=7
hay x=7/3(nhận)
23 tháng 5 2022
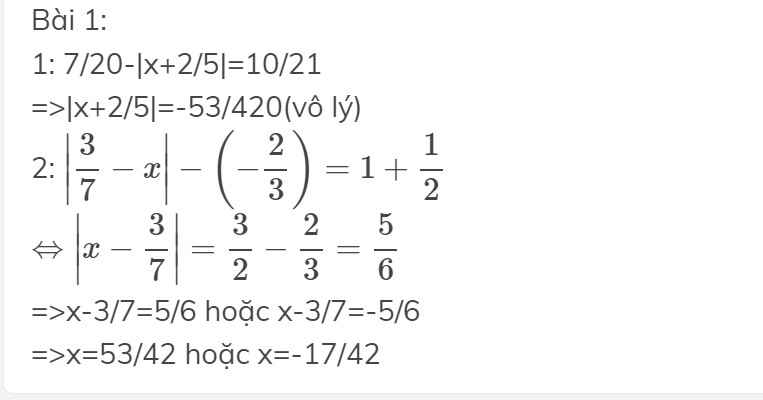
3: \(-\dfrac{1}{2}+\left|\dfrac{1}{3}x+\dfrac{2}{5}\right|=\dfrac{5}{7}\cdot\dfrac{3}{11}+\dfrac{8}{11}\cdot\dfrac{5}{7}=\dfrac{5}{7}\)
=>|1/3x+2/5|=5/7+1/2=17/14
=>1/3x+2/5=17/14 hoặc 1/3x+2/5=-17/14
=>x=171/70 hoặc x=-339/70
28 tháng 9 2019
1) \(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-24\)
\(=\left(x+2\right)\left(x+5\right)\left(x+3\right)\left(x+4\right)-24\)
\(=\left(x^2+7x+10\right)\left(x^2+7x+12\right)-24\)
Đặt \(x^2+7x=t\)
\(\Rightarrow BT=\left(t+10\right)\left(t+12\right)-24\)
\(=t^2+22x+96=\left(t+11\right)^2-25\ge-25\)
Vậy GTNN của bt là - 25\(\Leftrightarrow x^2+7x+11=0\)
\(\Delta=7^2-4.11=5\)
\(\orbr{\begin{cases}x_1=\frac{-22+\sqrt{5}}{2}\\x_2=\frac{-22-\sqrt{5}}{2}\end{cases}}\)
28 tháng 9 2019
2) \(\left(x-1\right)\left(x-3\right)\left(x-5\right)\left(x-7\right)-20\)
\(=\left(x-1\right)\left(x-7\right)\left(x-3\right)\left(x-5\right)-20\)
\(=\left(x^2-8x+7\right)\left(x^2-8x+15\right)-20\)
Đặt \(x^2-8x=t\)
\(\RightarrowĐT=\left(t+7\right)\left(t+15\right)-20\)
\(=t^2+22t+85=\left(t+11\right)^2-36\ge-36\)
Vậy GTNN của bt là - 36\(\Leftrightarrow x^2-8x+11=0\)
\(\Delta=\left(-8\right)^2-4.11=20\)
\(\orbr{\begin{cases}x_1=\frac{-22-\sqrt{20}}{2}\\x_2=\frac{-22+\sqrt{20}}{2}\end{cases}}\)
11 tháng 3 2023
`a,4x-10=0 `
`<=> 4x=10`
`<=>x=10/4`
`<=>x=5/2`
`b, 7-3x=9-x `
`<=>-3x+x=9-7`
`<=>-2x=2`
`<=>x=-1`
`c, 2x-(3-5x) = 4(x+3)`
`<=>2x-3+5x=4x+12`
`<=>2x+5x-4x=12+3`
`<=>3x=15`
`<=>x=5`
`d, 5-(6-x)=4(3-2x) `
`<=>5-6+x=12-8x`
`<=>x+8x=12-5+6`
`<=>9x=13`
`<=>x=13/9`
`e, 4(x+3)=-7x+17 `
`<=>4x+12=-7x+17`
`<=>4x+7x=17-12`
`<=>11x=5`
`<=>x=5/11`
`f, 5(x-3) - 4=2(x-1)+7`
`<=>5x-15-4=2x-2+7`
`<=>5x-2x=15+4-2+7`
`<=>3x=24`
`<=>x=8`
`g, 5(x-3)-4=2(x-1)+7 `
`<=>5x-15-4=2x-2+7`
`<=>5x-2x=15+4-2+7`
`<=>3x=24`
`<=>x=8`
`h,4(3x-2)-3(x-4)=7x+20`
`<=>12x-8-3x+12=7x+20`
`<=>12x-3x-7x=20+8+12`
`<=>2x=40`
`<=>x=20`
\(\left(x-1\right)\left(x-3\right)\left(x-5\right)\left(x-7\right)=20\\ \Leftrightarrow\left[\left(x-1\right)\left(x-7\right)\right]\left[\left(x-3\right)\left(x-5\right)\right]-20=0\\ \Leftrightarrow\left(x^2-8x+7\right)\left(x^2-8x+15\right)-20=0\\ \Leftrightarrow\left(x^2-8x+7\right)\left[\left(x^2-8x+7\right)+8\right]-20=0\\ \Leftrightarrow\left(x^2-8x+7\right)^2+8\left(x^2-8x+7\right)-20=0\\ \Leftrightarrow\left(x^2-8x+7\right)^2-2\left(x^2-8x+7\right)+10\left(x^2-8x+7\right)-20=0\\ \Leftrightarrow\left(x^2-8x+7\right)\left(x^2-8x+7-2\right)+10\left(x^2-8x+7-2\right)=0\)
\(\Leftrightarrow\left(x^2-8x+7+10\right)\left(x^2-8x+7-2\right)=0\\ \Leftrightarrow\left(x^2-8x+17\right)\left(x^2-8x+5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2-8x+16+1=0\\x^2-8x+16-11=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}\left(x-4\right)^2+1=0\left(vô.lí\right)\\\left(x-4\right)^2-11=0\end{matrix}\right.\\ \Leftrightarrow\left(x-4-\sqrt{11}\right)\left(x-4+\sqrt{11}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=4+\sqrt{11}\\x=4-\sqrt{11}\end{matrix}\right.\)
\(\left(x-1\right)\left(x-3\right)\left(x-5\right)\left(x-7\right)-20\)
\(=\left[\left(x-1\right)\left(x-7\right)\right]\left[\left(x-3\right)\left(x-5\right)\right]-20\)
\(=\left(x^2-8x+7\right)\left(x^2-8x+15\right)-20\)
Đặt \(x^2-8x+7=t\),ta có :
\(t\left(t+8\right)-20\)
\(=t^2+8t-20\)
\(=\left(t^2+8t+16\right)-16-20\)
\(=\left(t+4\right)^2-36\)
\(=\left(t+4\right)^2-6^2\)
\(=\left(t+4-6\right)\left(t+4+6\right)\)
\(=\left(t-2\right)\left(t+10\right)\)
\(=\left(x^2-8x+7-2\right)\left(x^2-8x+7+10\right)\)
\(=\left(x^2-8x+5\right)\left(x^2-8x+17\right)\)