Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

goi hai goc ke bu la goc ABC va MNP Ta co tia phan giac O cua goc ABC tao thanh hai goc ABO=CBO=1/2 ABC (1) Ta co tia phan giac I cua goc MNP tao thanh hai goc MNI=PNI=1/2 MNP (2) Tu (1) va (2) =>CBO+MNI=1/2 ABC+1/2 MNP=1/2(ABC+MNP)=1/2x90 do (DPCM)

Hướng dẫn:
a) Vì Ot là phân giác của ˆxOyxOy^
nên ˆyOtyOt^ = ˆxOtxOt^ = 1212ˆxOyxOy^
Ot' là phân giác của ˆxOy′xOy′^
nên ˆxOt′xOt′^ = ˆy′Ot′y′Ot′^ = 1212ˆxOy′xOy′^
=> ˆxOtxOt^ + ˆxOt′xOt′^ = 1212ˆxOyxOy^ + 1212ˆxOy′xOy′^ = 1212(ˆxOyxOy^ + ˆxOy′xOy′^)
mà (ˆxOyxOy^ + ˆxOy′xOy′^) = 1800 (2 góc kề bù)
=> ˆxOtxOt^ + ˆxOt′xOt′^ = 12121800 = 900
Vậy hai tia phân giác của hai góc kề bù tạo thành một góc vuông
b) Nếu M thuộc Ot hoặc Ot' thì M cách đều hai đường thẳng xx' và yy'
Thật vậy: M ε Ot do Ot là phân giác của ˆxOyxOy^ nên M cách đều Ox, Oy
=> M cách đều xx',yy'
M ε Ot'do Ot' là phân giác của ˆxOy′xOy′^ nên M cách đều xx', yy'
=> M cách đều xx',yy'
c) M cách đều hai đường thẳng xx', yy'
Nếu M nằm trong một góc trong bốn góc ˆxOyxOy^, ˆxOy′xOy′^, ˆx′Oy′x′Oy′^, ˆx′Oyx′Oy^ thì M phải thuộc phân giác của góc ây tức M phải thuộc Ot hoặc Ot'
d) Khi M ≡ O thì khoảng cách từ M đến xx', yy' bằng 0
e) Từ các câu trên ta có nhận xét: Tập hợp tất cả các điểm cách đều hai đường thẳng cắt nhau xx', yy' thuộc hai đường thẳng vuông góc nhau lần lượt là phân giác của các góc tạo bởi hai đường thẳng cắt nhau đó.
a) Vì Ot là phân giác của ˆxOyxOy^
nên ˆyOtyOt^ = ˆxOtxOt^ = 1212ˆxOyxOy^
Ot' là phân giác của ˆxOy′xOy′^
nên ˆxOt′xOt′^ = ˆy′Ot′y′Ot′^ = 1212ˆxOy′xOy′^
=> ˆxOtxOt^ +

x0y + y0z = 180
x0m = m0y = x0y/2 (1)
mà moy + yon = 90 (gt)
n0z + x0m = 90 ( vì m0n = 90)
từ (1) có yon = n0z hay on là phân giác của yoz

t x z y h ? 20* 20* 70*
Vì Oh là tia phân giác của \(\widehat{xOy}\)
\(\Rightarrow\) \(\widehat{xOh}\) = \(\widehat{hOy}\) \(\frac{\widehat{xOy}}{2}\) = \(\frac{\widehat{40^0}}{2}\) = 20*
\(\Rightarrow\) \(\widehat{hOy}\) + \(\widehat{yOz}\) = \(\frac{\widehat{yOz}}{2}\) + \(\frac{\widehat{yOt}}{2}\)
\(\Rightarrow\) \(\widehat{hOy}\) + \(\widehat{zOy}\) = \(\frac{\widehat{yOz}+\widehat{yOt}}{2}\)
\(\Rightarrow\) \(\widehat{hOy}\) + \(\widehat{yOz}\) = \(\frac{180^0}{2}\) = 90* ( Vì \(\widehat{xOy}\) và \(\widehat{yOt}\) là 2 góc kề bù )
hay \(\widehat{hOz}\) = 90*
Vậy Oh vuông góc với Oz

x O z y m n
Om là phân giác góc xOy
=> góc mOy = 1/2 góc xOy
On là phân giác góc yOz
=> góc yOn = 1/2 góc yoz
suy ra: góc mOy + góc yOn = 1/2 (góc xOy + góc yOz)
<=> góc mOn = 1/2.1800 = 900 (do góc xOy và góc yOz kề bù)
Om phân giác xoy => moy=1/2xoy hay xoy=2moy
tương tự => noy=1/2yoz hay yoz=2noy
Lại có:
xoy+yoz=180
=>2moy +2noy=180
=>moy+noy=90 hay mon =90

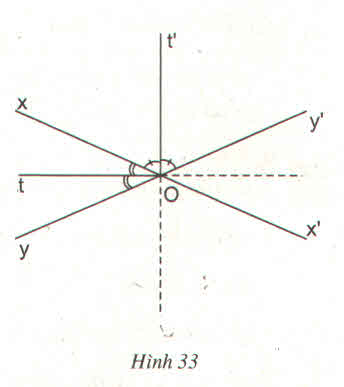
Chứng minh:
1) ∠tOy = 1/2. ∠xOy = 1/2. mo (Vì Ot là tia phân giác của góc xOy)
4) ∠x'Oy = 180o - ∠xOy = 180o - mo (Vì ∠x'Oy và ∠xOy kề bù)
2) ⇒ ∠t'Oy = 1/2. ∠x'Oy = 1/2. (180o - mo) (Vì Ot’ là phân giác của ∠x'Oy)
3) ⇒ ∠tOt' = ∠tOy + ∠t'Oy = 1/2. mo + 1/2. (180o - mo) = 90o.
Kết luận: Vậy hai tia phân giác của hai góc kề bù tạo thành góc vuông.